Angle Between Two Lines
Whenever two straight lines intersect, they form two sets of angles. The intersection forms a pair of acute and another pair of obtuse angles. The absolute values of angles formed depend on the slopes of the intersecting lines.
It is also worth noting here that the angle formed by the intersection of two lines cannot be calculated if one of the lines is parallel to the y-axis as the slope of a line parallel to the y-axis is an indeterminate.
Angle Between Two Straight Lines Formula
If θ is the angle between two intersecting lines defined by y1= m1x1+c1 and y2= m2x2+c2, then, the angle θ is given by
tanθ=±(m2-m1) / (1+m1m2)
Angle Between Two Straight Lines Derivation
Consider the diagram below:
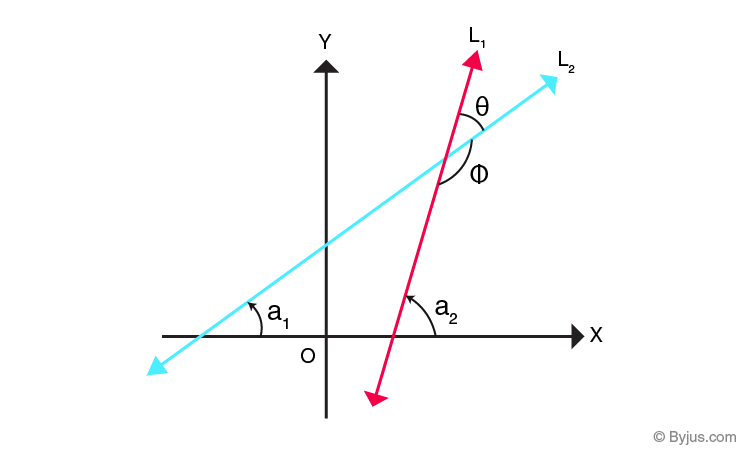
In the diagram above, the line L1 and line L2 intersect at a point.
Let the slope measurement can be taken as
tan a1 = m1 and tan a2 = m2
Also, from the figure, we can infer that θ = a2-a1
Now, tan θ = tan (a2-a1) = (tan a2 – tan a1 ) / (1- tan a1tan a2)
Substituting the values of tan a1 and tan a2 as m1 and m2 respectively, we have,
tanθ= (m2 – m1 ) / (1+m1m2)
It should be noted that the value of tan θ in this equation will be positive if θ is acute and negative if θ is obtuse.
Angle Between Two Lines Coordinate Geometry
In analytic geometry, if the coordinates of three points A, B, and C are given, then the angle between the lines AB and BC can be calculated as follows:
For a line whose endpoints are (x1, y1) and (x2, y2), the slope of the line is given by the equation
m = \(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
The angle between the two lines can be found by calculating the slope of each line and then using them in the formula to determine the angle between two lines when the slope of each line is known from the equation
tan θ=± (m1 – m2 ) / (1+ m1m2)
We shall explore solved numerical problems in the next section.
Problem With Solution
If P (-2, 1), Q (2, 3) and R (-2, -4) are three points, find the angle between the straight lines PQ and QR.
The slope of PQ is given by
m = ( y2 – y1 ) / (x2 – x1)
m =( 3 – 1 ) / (2 – (-2 ))
m= 2/4
Therefore, m1=1/2
The slope of QR is given by
m= (−4−3) / (−2−2)
m= 7/4
Therefore, m2 = 7/4
Substituting the values of m2 and m1 in the formula for the angle between two lines when we know the slopes of two sides, we have,
tan θ=± (m2 – m1 ) / (1+m1m2)
tan θ=± ((7/4) – (1/2) ) / (1+ (1/2)(7/4))
tan θ=± (2/3)
Therefore, θ = tan -1 (⅔)
Learn more about the angle between two lines and related topics from analytic geometry in a simple way. Register with BYJU’S – The Learning App today.
| Related Links | |
| Coordinate Geometry Formulas For Class 11 | Coordinate System |
| Circles in Coordinate Geometry | Two Dimensional Coordinate Geometry |