Determinant of a 3 x 3 matrix
In matrices, determinants are the special numbers calculated from the square matrix. The determinant of a 3 x 3 matrix is calculated for a matrix having 3 rows and 3 columns. The symbol used to represent the determinant is represented by vertical lines on either side, such as | |. The most popular application is to find area of triangle using determinant, where the three vertices of the triangle are considered as the coordinates in an XY plane.
Let A be the matrix, then the determinant of a matrix A is denoted by |A|. To find any matrix such as determinant of 2×2 matrix, determinant of 3×3 matrix, or n x n matrix, the matrix should be a square matrix. It means that the matrix should have an equal number of rows and columns. Finding determinants of a matrix are helpful in solving the inverse of a matrix, a system of linear equations, and so on. In this article, let us discuss how to solve the determinant of a 3×3 matrix with its formula and examples.
Determinant of a 3 x 3 Matrix Formula
We can find the determinant of a matrix in various ways. First, we have to break the given matrix into 2 x 2 determinants so that it will be easy to find the determinant for a 3 by 3 matrix.
Let’s suppose you are given a square matrix C where
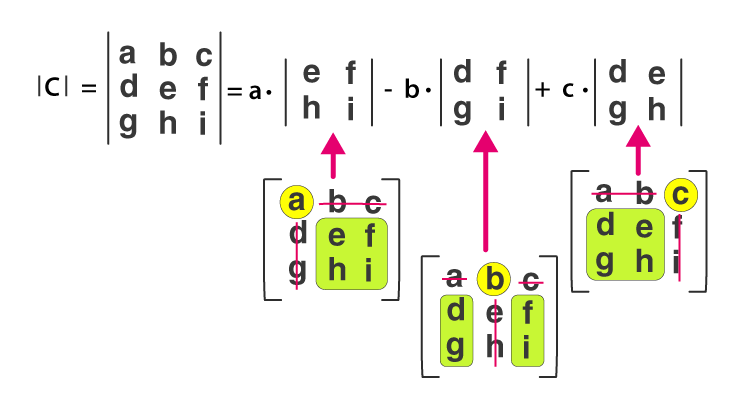
C = \(\begin{bmatrix} a & b &c \\ d& e &f \\ g& h &i \end{bmatrix}\)
Let’s calculate the determinant of matrix C,
Det \(\begin{bmatrix} a & b &c \\ d& e &f \\ g& h &i \end{bmatrix}\)
= a. det \(\begin{bmatrix} e & f\\ h & i \end{bmatrix}\) – b.det \(\begin{bmatrix} d & f\\ g & i \end{bmatrix}\) + c . det \(\begin{bmatrix} d & e\\ g & h \end{bmatrix}\)
Few Important points on 3x 3 Determinant Matrix:
- The scalar multipliers to a corresponding 2 x 2 matrix have top row elements a, b and c serving to it.
- The scalar element gets multiplied by 2 x 2 matrix of remaining elements created at the time when vertical and horizontal line segments were drawn through passing through a.
- This is how we construct the 2 by 2 matrices for scalar multipliers b and c.
The determinant of 3 x 3 matrix formula is given by,
\(\begin{bmatrix} a & b &c \\ d& e &f \\ g& h &i \end{bmatrix}\) = \(\begin{bmatrix} 2 & -3 &9 \\ 2 & 0 & -1\\ 1& 4 & 5 \end{bmatrix}\)
Examples
Let us solve some examples to find the determinant of some of the matrices having three rows and columns.
Example 1: Calculate the determinant of the 3 x 3 matrix.
\(\begin{bmatrix} 2 & -3 &1 \\ 2 & 0 & -1\\ 1& 4 & 5 \end{bmatrix}\)
Solution:
Let’s find the correspondence between the generic elements in the formula and elements of real problem.
\(\begin{bmatrix} a & b &c \\ d& e &f \\ g& h &i \end{bmatrix}\) = \(\begin{bmatrix} 2 & -3 &1 \\ 2 & 0 & -1\\ 1& 4 & 5 \end{bmatrix}\)Use the 3 x 3 determinant formula:
Applying the formula,

= 2[ 0 – (-4)] + 3 [10 – (-1)] +1 [8-0]
= 2 (0+4) +3 (10 +1) + 1(8)
= 2(4) +3(11) + 8
= 8+33+8
= 49
Therefore, the determinant of \(\begin{bmatrix} 2 & -3 &9 \\ 2 & 0 & -1\\ 1& 4 & 5 \end{bmatrix}\) = 49
Example 2: Calculate the determinant of the 3 x 3 matrix.
\(\begin{bmatrix} 1 & 3 &2 \\ -3 & -1 & -3\\ 2& 3 & 1 \end{bmatrix}\)
Solution:
Let’s find the correspondence between the generic elements in the formula and elements of real problem.
\(\begin{bmatrix} a & b &c \\ d& e &f \\ g& h &i \end{bmatrix}\) = \(\begin{bmatrix} 1 & 3 &2 \\ -3 & -1 & -3\\ 2& 3 & 1 \end{bmatrix}\)Use the 3 x 3 determinant formula:
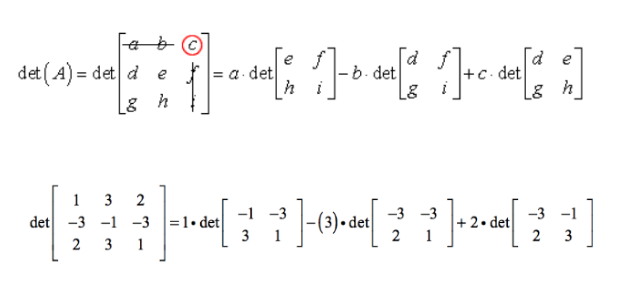
= 1[ -1 – (-9)] – 3 [-3 – (-6)] + 2 [-9 – (-2)]
= 1 (-1+9) -3 (-3 +6) + 2(-9 + 2)
= 1(8) -3(3) +2(-7)
= 8 -9-14
= -15
Therefore, the determinant of \(\begin{bmatrix} 1 & 3 &2 \\ -3 & -1 & -3\\ 2& 3 & 1 \end{bmatrix}\) =-15
Found this topic interesting, explore more on other mathematical topics on BYJU’S- The Learning App.
| Learn more on Matrices | |
| Determinant Formula | Inverse Matrix Formulas |
| Determinants and Matrices | Determinants for Class 12 |