Lognormal Distribution
A probability distribution of outcomes which is symmetrical or forms a bell curve is called a normal distribution. A log-normal distribution can be formed from a normal distribution using logarithmic mathematics. The continuous probability distribution of a random variable whose logarithm is normally distributed is called a lognormal distribution. A random variable of lognormal distribution takes only positive real values.
Lognormal distribution of a random variable
If X is a random variable and Y=ln(X) is normally distributed, then X is said to be distributed lognormally. Similarly, if Y has a normal distribution, then the exponential function of Y will be having a lognormal distribution, i.e. X=exp(Y). A statistical result of the multiplicative product of many independent random variables, each of which is positive is considered as a lognormal process.
What type of data is suitable?
All positive values, skewed distributions with low mean values and large variance. Since, only for positive values, log(x) exists.
Probability density function
A random variable X is distributed log-normally if and only if the logarithm of X is normally distributed. Also, the value of X should be positive.
The lognormal distribution is a two-parameter distribution with parameters μ and σ. The probability density function can be defined as:

Here, t values are the time-to-failure
Mean of the natural logarithms of the time-to-failure
Standard deviation (SD) of the natural logarithms of the time-to-failure
The lognormal probability distribution can be obtained on realizing that, for equal probabilities under the normal and lognormal probability distribution, incremental areas should also be equal.
Now,
 …..(i)
…..(i)
On applying the derivative, we get
 ….(ii)
….(ii)
From (i) and (ii),

Mean of Lognormal distribution
The major lognormal distribution functions are:
- Mean
The mean of a lognormal distribution of

The mean of the natural logarithms of time-to-failure

- Median

- Mode

- Standard deviation
- The lognormal reliability function
- The lognormal conditional reliability function
- The lognormal reliable life function
- The lognormal failure rate function
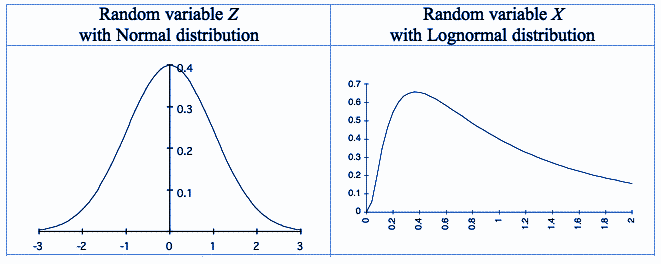
Lognormal distribution curve
It is skewed towards the right.
The value of probability distribution function starts at zero, increases and then decreases.
If increases for a given , then the degree of skewness will increase.
For the same , if increases, then the probability distribution function’s skewness will also increase.
The following three parameters are responsible for the shape of a lognormal distribution.
Shape parameter
The standard deviation for the lognormal affects the general shape of the distribution. The shape parameter doesn’t change the location or height of the graph; it just affects the overall shape.
Scale parameter
It is the median, it tends to shrink or stretch the graph.
Location parameter
It tells us where the graph is located on the x-axis.
Read more:
Applications of Lognormal distribution
- Rubik’s Cube solves, both general or by a person, appear to be following a lognormal distribution
- The length of comments posted on social media website discussion forums follows a lognormal distribution
- Time spent by a user on online articles (jokes, news etc.) follows a lognormal distribution
- In economics, to analyse the income of the population other than higher-income individuals
- In order to analyse the fluctuations in the stock markets
Lognormal distribution Table


