A function is said to be continuous if it can be drawn without picking up the pencil. Otherwise, a function is said to be discontinuous. Similarly, Calculus in Maths, a function f(x) is continuous at x = c, if there is no break in the graph of the given function at the point. (c, f(c)). In this article, let us discuss the continuity and discontinuity of a function, different types of continuity and discontinuity, conditions, and examples.

Continuity Definition

A function is said to be continuous in a given interval if there is no break in the graph of the function in the entire interval range. Assume that “f” be a real function on a subset of the real numbers and “c” be a point in the domain of f. Then f is continuous at c if

\(\lim_{x\rightarrow c}f(x)= f(c)\)

In other words, if the left-hand limit, right-hand limit and the value of the function at x = c exist and are equal to each other, i.e.,

\(\lim_{x\rightarrow c^{-}}f(x)= f(c)=\lim_{x\rightarrow c^{+}}f(x)\),

then f is said to be continuous at x = c

Conditions for Continuity

• A function “f” is said to be continuous in an open interval (a, b) if it is continuous at every point in this interval.
• A function “f” is said to be continuous in a closed interval [a, b] if
  • f is continuous in (a, b)
  • \(\lim_{x\rightarrow a^{+}}f(x)= f(a)\)
  • \(\lim_{x\rightarrow b^{-}}f(x)= f(b)\)

Discontinuity Definition

The function “f” will be discontinuous at x = a in any of the following cases:

• f (a) is not defined.
• \(\lim_{x\rightarrow a^{-}}f(x)\) and \(\lim_{x\rightarrow a^{+}}f(x)\) exist but are not equal.
• \(\lim_{x\rightarrow a^{-}}f(x)\) and \(\lim_{x\rightarrow a^{+}}f(x)\) exist and are equal but not equal to f (a).

Types of Discontinuity

The four different types of discontinuities are:

• Removable Discontinuity
• Jump Discontinuity
• Infinite Discontinuity

Let’s discuss the different types of discontinuity in detail.

Removable Discontinuity

In removable discontinuity, a function which has well- defined two-sided limits at x = a, but either f(a) is not defined or f(a) is not equal to its limits. The removable discontinuity can be given as:

\(\lim_{x\rightarrow a}f(x)\neq f(a)\)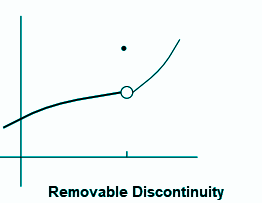

This type of discontinuity can be easily eliminated by redefining the function in such a way that

\(f(a) = \lim_{x\rightarrow a}f(x)\)

Jump Discontinuity

Jump Discontinuity is a type of discontinuity, in which the left-hand limit and right-hand limit for a function x = a exists, but they are not equal to each other. The jump discontinuity can be represented as:

\(\lim_{x\rightarrow a^{+}}f(x)\neq \lim_{x\rightarrow a^{-}}f(x)\)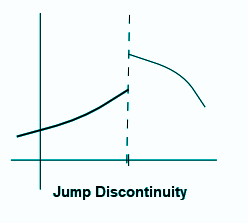

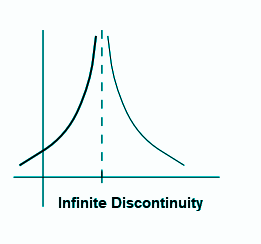
Infinite Discontinuity

In infinite discontinuity, the function diverges at x =a to give a discontinuous nature. It means that the function f(a) is not defined. Since the value of the function at x = a does not approach any finite value or tends to infinity, the limit of a function x → a are also not defined.

Continuity and Discontinuity Examples

Go through the continuity and discontinuity examples given below.

Example 1:

Discuss the continuity of the function f(x) = sin x . cos x.

Solution:

We know that sin x and cos x are the continuous function, the product of sin x and cos x should also be a continuous function.

Hence, f(x) = sin x . cos x is a continuous function.

Example 2:

Prove that the function f is defined by \(f(x)= \left\{\begin{matrix} x sin\frac{1}{x} & x\neq 0\\ 0 & x=0 \end{matrix}\right.\) is continuous at x =0

Solution:

Left hand limit at x = 0 is given by

\(\lim_{x\rightarrow 0^{-}}f(x) = \lim_{x\rightarrow 0^{-}}xsin\frac{1}{x}=0\) [Since -1Similarly, \(\lim_{x\rightarrow 0^{+}}f(x) = \lim_{x\rightarrow 0^{+}}xsin\frac{1}{x}=0\), [f(0) =0]

Thus, \(\lim_{x\rightarrow 0^{-}}f(x) = \lim_{x\rightarrow 0^{+}}f(x) = f(0)\).

Hence, the function f(x) is continuous at x =0.

Stay tuned with BYJU’S- The Learning App and download the app to get the interactive videos to learn with ease.