Analytic Geometry
Analytic Geometry is a branch of algebra, a great invention of Descartes and Fermat, which deals with the modelling of some geometrical objects, such as lines, points, curves, and so on. It is a mathematical subject that uses algebraic symbolism and methods to solve the problems. It establishes the correspondence between the algebraic equations and the geometric curves. The alternate term which is used to represent the analytic geometry is “coordinate Geometry”.
It covers some important topics such as midpoints and distance, parallel and perpendicular lines on the coordinate plane, dividing line segments, distance between the line and a point, and so on. The study of analytic geometry is important as it gives the knowledge for the next level of mathematics. It is the traditional way of learning the logical thinking and the problem solving skills. In this article, let us discuss the terms used in the analytic geometry, formulas, Cartesian plane, analytic geometry in three dimensions, its applications, and some solved problems.
Table of Contents:
- Definition
- Planes
- Coordinates
- Cartesian Plane
- Formulas
- Analytic Geometry in 3D
- Applications
- Problems
- FAQs
What is Analytic Geometry?
Analytic geometry is that branch of Algebra in which the position of the point on the plane can be located using an ordered pair of numbers called as Coordinates. This is also called coordinate geometry or the Cartesian geometry. Analytic geometry is a contradiction to the synthetic geometry, where there is no use of coordinates or formulas. It is considered axiom or assumptions, to solve the problems. But in analytic geometry, it defines the geometrical objects using the local coordinates. It also uses algebra to define this geometry.
Coordinate geometry has its use in both two dimensional and three-dimensional geometry. It is used to represent geometrical shapes. Let us learn the terminologies used in analytic geometry, such as;
- Plane
- Coordinates
Planes
To understand how analytic geometry is important and useful, First, We need to learn what a plane is? If a flat surface goes on infinitely in both the directions, it is called a Plane. So, if you find any point on this plane, it is easy to locate it using Analytic Geometry. You just need to know the coordinates of the point in X and Y plane.
Coordinates
Coordinates are the two ordered pair, which defines the location of any given point in a plane. Let’s understand it with the help of the box below.
| A | B | C | |
| 1 | |||
| 2 | x | ||
| 3 |
In the above grid, The columns are labelled as A, B, C, and the rows are labelled as 1, 2, 3.
The location of letter x is B2 i.e. Column B and row 2. So, B and 2 are the coordinates of this box, x.
As there are several boxes in every column and rows, but only one box has the point x, and we can find its location by locating the intersection of row and column of that box. There are different types of coordinates in analytical geometry. Some of them are as follows:
- Cartesian Coordinates
- Polar Coordinates
- Cylindrical Coordinates
- Spherical Coordinates
Let us discuss all these types of coordinates are here in brief.
Cartesian Coordinates
The most well-known coordinate system is the Cartesian coordinate to use, where every point has an x-coordinate and y-coordinate expressing its horizontal position, and vertical position respectively. They are usually addressed as an ordered pair and denoted as (x, y). We can also use this system for three-dimensional geometry, where every point is represented by an ordered triple of coordinates (x, y, z) in Euclidean space.
Polar Coordinates
In the case of polar coordinates, each point in a plane is denoted by the distance ‘r’ from the origin and the angle θ from the polar axis.
Cylindrical Coordinates
In the case of cylindrical coordinates, all the points are represented by their height, radius from z-axis and the angle projected on the xy-plane with respect to the horizontal axis. The height, radius and the angle are denoted by h, r and θ, respectively.
Spherical Coordinates
In spherical coordinates, the point in space is denoted by its distance from the origin ( ρ), the angle projected on the xy-plane with respect to the horizontal axis (θ), and another angle with respect to the z-axis (φ).
Cartesian Plane
In coordinate geometry, every point is said to be located on the coordinate plane or cartesian plane only.
Look at the figure below.
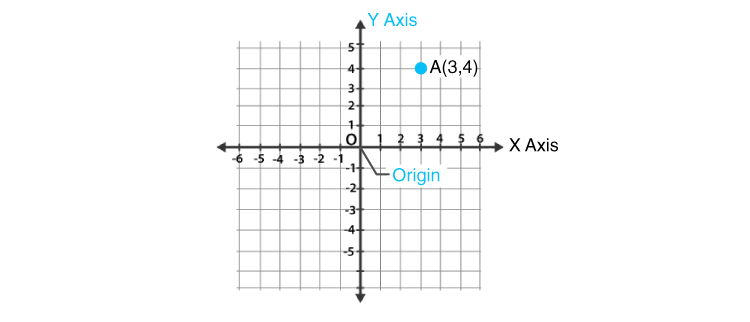
The above graph has x-axis and y-axis as it’s Scale. The x-axis is running across the plane and Y-axis is running at the right angle to the x-axis. It is similar to the box explained above.
Let’s learn more about Co-ordinates:
Origin: It is the point of intersection of the axis(x-axis and y-axis). Both x and y-axis are zero at this point.
Values of the different sides of the axis:
x-axis – The values at the right-hand side of this axis are positive and those on the left-hand side are negative.
y-axis – The values above the origin are positive and below the origin are negative.
To locate a point: We need two numbers to locate a plane in the order of writing the location of X-axis first and Y-axis next. Both will tell the single and unique position on the plane. You need to compulsorily follow the order of the points on the plane i.e., the x coordinate is always the first one from the pair. (x, y).
If you look at the figure above, point A has a value 3 on the x-axis and value 2 on the Y-axis. These are the rectangular coordinates of Point A represented as (3, 2).
Using the Cartesian coordinates, we can define the equation of a straight lines, equation of planes, squares and most frequently in the three dimensional geometry. The main function of the analytic geometry is that it defines and represents the various geometrical shapes in the numerical way. It also extracts the numerical information from the shapes.
Read: Analytic Function
Analytic Geometry Formulas
Graphs and coordinates are used to find measurements of geometric figures. There are many important formulas in analytic Geometry. Since science and engineering involves the study of rate of change in varying quantities, it helps to show the relation between the quantities involved. The branch of Mathematics called “calculus” requires the clear understanding of the analytic geometry. Here, some of the important ones are being used to find the distance, slope or to find the equation of the line.
Distance Formula
Let the two points be A and B, having coordinates to be (x1, y1) and (x2, y2) respectively.
Thus, the distance between two points is given as-
d = √[(x2-x1)2+(y2-y1)2]
Midpoint Theorem Formula
Let A and B are some points in a plane, which is joined to form a line, having coordinates (x1, y1) and (x2, y2), respectively. Suppose, M(x, y) is the midpoint of the line connecting the point A and B then its formula is given by;
M(x, y) = [(x1+x2)/2, (y1+y2)/2)]
Angle Formula
Let two lines have slope m1 and m2 and θ is the angle formed between the two lines A and B, which is represented as;
tan θ = (m1-m2)/ (1+m1m2)
Section Formula
Let two lines A and B have coordinates (x1, y1) and (x2, y2), respectively. A point P the two lines in the ratio of m:n, then the coordinates of P is given by;
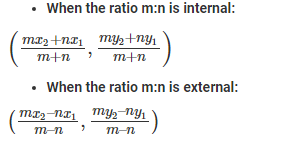
Analytic Geometry in Three Dimensions
In this, we consider triples (a, b, c) which are real numbers and call this set as three- dimensional number space and denote it by R’. All the elements in the triple are called coordinates.
Let’s see how three-dimensional number space is represented on a geometric space.
In three-dimensional space, we consider three mutually perpendicular lines intersecting in a point O. these lines are designated coordinate axes, starting from 0, and identical number scales are set up on each of them.
Learn more on Coordinate Geometry in Two Dimensional Plane
Analytic Geometry Applications
Analytic geometry is widely used in the fields such as Engineering and Physics. Also, it is widely used in the fields such as space science, rocket science, aviation, space flights and so on. Analytical geometry has made many things possible like the following:
- We can find whether the given lines are perpendicular or parallel.
- We can determine the mid-point, equation, and slope of the line segment.
- We can find the distance between the points.
- We can also determine the perimeter of the area of the polygon formed by the points on the plane.
- Define the equations of ellipse, curves, and circles.
Analytic Geometry Problems
Example 1:
What is the point of intersection of the axis (X-axis and Y-axis) called?
Solution:
The point of intersection of the axis (X-axis and Y-axis) called Origin and X and the Y-axis is 0 at this point.
Example 2:
Find the distance between two points A and B such that the coordinates of A and B are (5, -3) and (2, 1).
Solution:
Given that, the coordinates are:
A = (5, -3) = (x1, y1)
B = (2, 1) = (x2, y2)
The formula to find the distance between two points is given as:
Distance, d = √[(x2– x1)2 + (y2– y1)2]
d = √[(2 – 5)2 + (1- (-3))2]
d = √[(-3)2 + (4)2]
d = √[9 + 16]
d = √(25)
d = 5
Thus, the distance between two points A and B is 5 units.
Example 3:
Determine the slope of the line, that passes through the point A(5, -3), and it meets y-axis at 7.
Solution:
Given that, the point is A = (5, -3)
We know that, if the line intercepts at y-axis, then x2 = 0
Thus, (x2, y2) = (0, 7)
The formula to find the slope of a line is:
m = (y2 –y1)/ (x2 -x1)
Now, substitute the values
m = (7- (-3))/(0 – 5)
m = 10/-5
m = -2
Therefore, the slope of the line is -2.
Find more Maths topic on BYJU’S – The Learning App. Also, subscribe to BYJU’S YouTube channel and get videos on numerous mathematical concepts explained in an engaging and effective way.