SSS Congruence rule: If three sides of one triangle are equal to the corresponding sides of another triangle, then the triangles are congruent. Constructing triangles using SSS congruence criteria is possible when all the three sides are known to us. The requirements for construction are: A ruler and a compass. Side-Side-Side is one of the properties of similar triangles.

How to construct a triangle with the given three sides?

By SSS rule, construction of a triangle is possible with three given side measures. For the construction of a triangle, first identify the longest measure among the three side measures. Draw the longest side measure as the base of the triangle, then take other measurements using a ruler to mark the arcs by taking the endpoints of the base as vertices. Finally, join the intersection of arcs with the endpoints of the base to get the required triangle.

Constructing SSS Triangles

Let us consider a triangle ABC, having the measurement of sides equal: AB = 7 cm, BC = 4 cm and CA = 6 cm. The steps for construction of triangle are:

• Step 1: Mark a point A
• Step 2: Measure the length of 7 cm using compass and scale
• Step 3: With the help of Compass mark an arc placing pointer at point A
• Step 4: Mark a point B on the arc

• Step 5: Now measure the length of 6 cm
• Step 6: Again using compass mark an arc above point B using the same point (A)

• Step 7: Measure the length of 4 cm
• Step 8: Using the compass placed at point B cut an arc such that it crosses the previous arc.

• Step 9: Name the point as C where the two arcs cross each other
• Step 10: At the end, join the points A, B and C with the help of a ruler to give the required triangle.

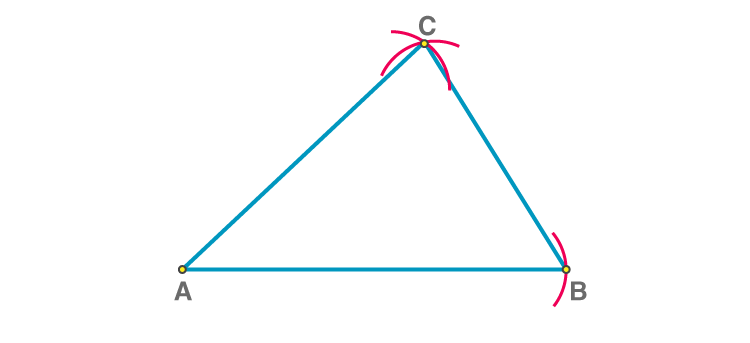
Thus, the obtained triangle is the required triangle ABC with the given measurements.

To learn more about constructing triangles, download BYJU’S-The Learning App.