Construction of rhombus will explain here how to draw a rhombus with the given combination of measurements, such as:

• Length of its two diagonals
• Length of its side and measure of one angle
• Length of its side and one diagonal

Before talking about the construction of rhombus, let us recall the properties of a rhombus. A rhombus is a quadrilateral that has all its four sides equal in length. The diagonals of the rhombus bisect each other at a right angle. Also, the opposite angles of a rhombus are equal in measure and opposite sides are parallel to each other.

In this article, we will discuss steps to construct a rhombus, where the measurement of its two diagonals is given. Class 8 students can learn to construct a rhombus with the simple steps given here.

Construction of Rhombus Given Length of Two Diagonals

A rhombus is a quadrilateral with sides of equal length. Opposite sides are parallel and opposite vertex angles are equal. Let us say, you are required to construct a rhombus PQRS with the lengths of its two diagonals, PR = 6 cm and SQ = 7 cm. We know that the diagonals of a rhombus bisect each other at 90 degrees. Hence, we do not require any other dimension for the construction of rhombus. The steps are:

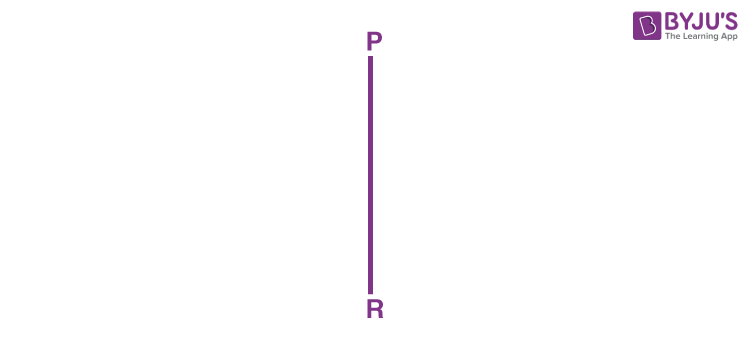
Step 1: Draw a vertical line segment PR of length 6 cm.

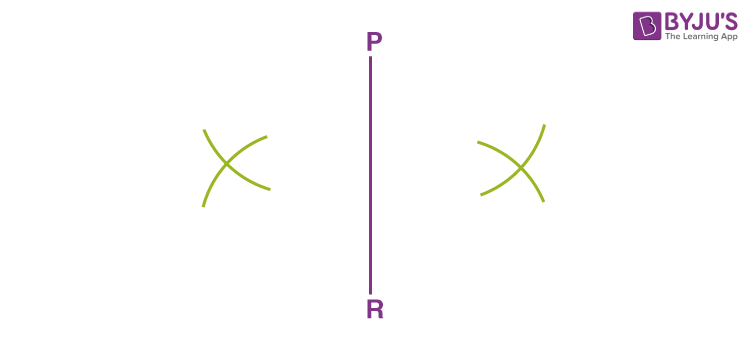
Step 2: Take the compass of any radius and from the point P, mark an arc towards the left and the other towards the right of PR. Repeat the same from point R without changing the compass radius.

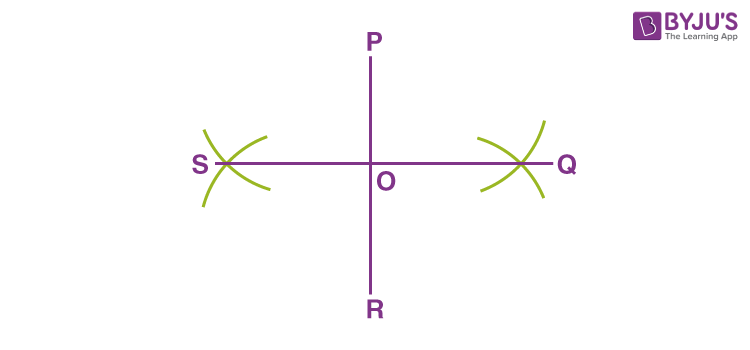
Step 3: The other diagonal measures 7 cm. Thus, draw a line joining the two points where the arc intersected each other in such a way that OS = OQ = 7/2 = 3.5 cm

Step 4: Join the point P with Q, Q with R, R with S and S with P.

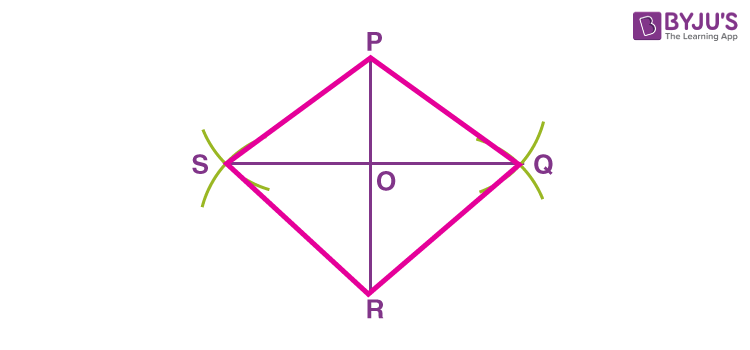
PQRS is the required rhombus with the diagonals of lengths 6 cm and 7 cm. Note that O is the mid-point of the two diagonals and ∠POQ = ∠QOR = ∠ROS = ∠SOP = 90 degrees.

Construction of Rhombus Given One Side and One Angle

If we are provided with one side and one angle of a rhombus, then follow the below steps to construct the rhombus.

• Draw the line segment of the given length, say AB
• At one endpoint of the line segment, draw an angle of a given measure, say ∠BAX
• With A as center and length equal to AB, draw an arc cutting the ray AX at D
• Now with D as center and radius equal to AB, draw an arc
• Taking B as center and with same radius, cut the previous arc at C
• Now join DC and BC

Hence, ABCD is the required rhombus.

An example figure is given below.

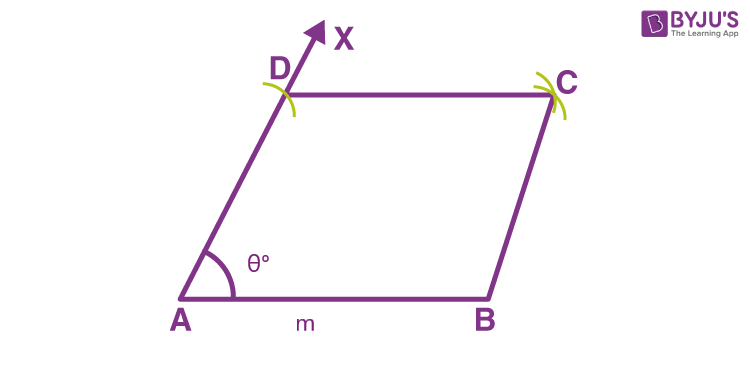
Construction of Rhombus Given one Diagonal and one Side

If we are given with length of one diagonal and one side, then we can construct a rhombus following the below steps:

• Draw a line segment AB equal to the length of the given side of the rhombus
• With A as center and radius equal to the length of diagonal draw an arc on the right side of point A and above B
• With B as center and radius equal to AB, cut the previous arc at C
• With C as center and radius equal to AB, draw an arc
• With A as center and same radius, cut the previous arc at D
• Join AD, BC and CD

Hence, ABCD is the required rhombus.

An example figure is given below.

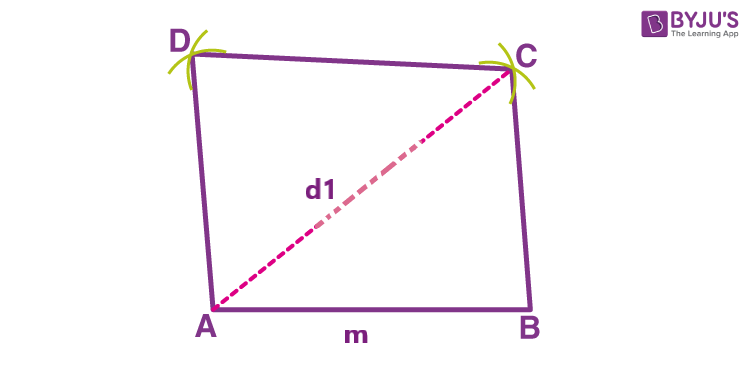
Related Articles

• Properties of Rhombus
• Construction Of Quadrilaterals
• Construction Of Square
• Constructing Triangles
• Construction Of Angles
• Construction Of Similar Triangles

Practice Questions

Here are some sample questions, students can practice drawing a rhombus.

1. Construct a rhombus with side PQ = 6 cm and angle P = 60 degrees
2. Construct a rhombus, with the length of one diagonal equal to 4.4 cm and another diagonal equal to 8 cm.