Constructions Class 10 Notes: Chapter 11
CBSE Class 10 Maths Construction Notes:-Download PDF Here
The construction for class 10 Maths notes are provided here. These notes help for the revision of concepts for the CBSE Class 10 Board Exams 2021-22. In this article, we will discuss how to construct the division of the line segment, constructions of tringles using scale factor, construction of tangents to a circle with two different cases are discussed here in detail. Go through the below article, to learn the construction procedure.
Dividing a Line Segment
Bisecting a Line Segment
Step 1: With a radius of more than half the length of the line segment, draw arcs centred at either end of the line segment so that they intersect on either side of the line segment.
Step 2: Join the points of intersection. The line segment is bisected by the line segment joining the points of intersection.

PQ is the perpendicular bisector of AB
2) Given a line segment AB, divide it in the ratio m:n, where both m and n are positive integers.
Suppose we want to divide AB in the ratio 3:2 (m=3, n=2)
Step 1: Draw any ray AX, making an acute angle with line segment AB.
Step 2: Locate 5 (= m + n) points A1,A2,A3,A4andA5 on AX such that AA1=A1A2=A2A3=A3A4=A4A5
Step 3: Join BA5.(A(m+n)=A5)
Step 4: Through the point A3(m=3), draw a line parallel to BA5 (by making an angle equal to ∠AA5B) at A3 intersecting AB at point C.
Then, AC : CB = 3 : 2.
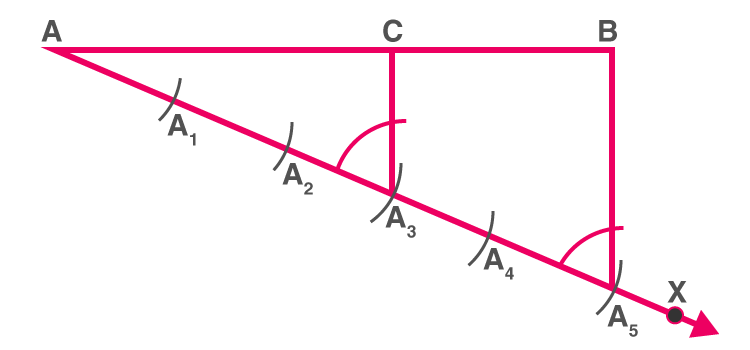
Division of a line segment
To know more about Dividing a Line Segment, visit here.
Constructing Similar Triangles
Constructing a Similar Triangle with a scale factor
Suppose we want to construct a triangle whose sides are 3/4 times the corresponding sides of a given triangle

Steps of Construction:
Step 1: Draw any ray BX making an acute angle with side BC (on the side opposite to the vertex A).
Step 2: Mark 4 consecutive distances(since the denominator of the required ratio is 4) on BX as shown.
Step 3: Join B4C as shown in the figure.
Step 4: Draw a line through B3 parallel to B4C to intersect BC at C’.
Step 5: Draw a line through C’ parallel to AC to intersect AB at A’. ΔA′BC′ is the required triangle.
The same procedure can be followed when the scale factor > 1.
To know more about Constructing Similar Triangles, visit here.
There are two cases while constructing a triangle similar to a given triangle as per the given scale factor. They are:
Case 1: The triangle to be constructed is smaller than the given triangle, and the scale factor is less than 1.
Case 2: The triangle to be constructed is larger than the given triangle, and the scale factor is greater than 1.
Here, the scale factor means the ratio of the triangle sides to be constructed with the corresponding sides of the given triangle.
Drawing Tangents to a Circle
Tangents: Definition
A tangent to a circle is a line which touches the circle at exactly one point.
For every point on the circle, there is a unique tangent passing through it.
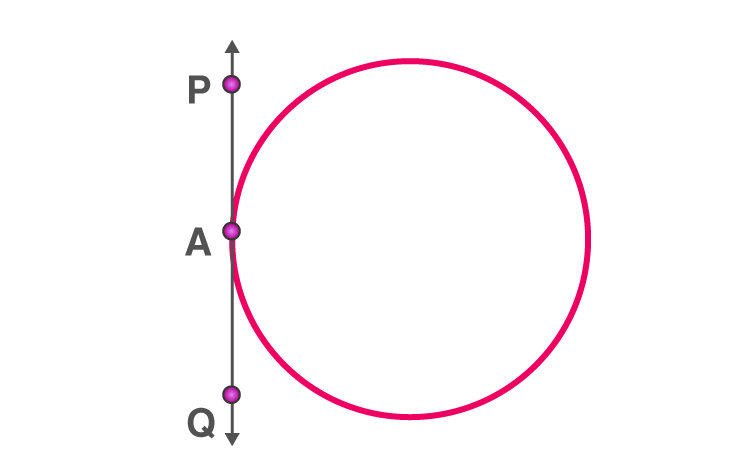
PQ is the tangent, touching the circle at A
To know more about Drawing Tangents to a Circle, visit here.
Number of Tangents to a circle from a given point
i) If the point is in an interior region of the circle, any line through that point will be a secant. So, in this case, there is no tangent to the circle.

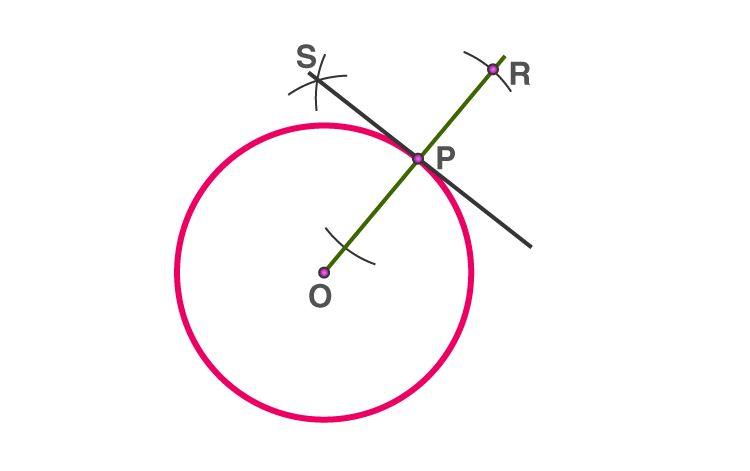
AB is a secant drawn through the point S
ii) When the point lies on the circle, there is accurately only one tangent to a circle.
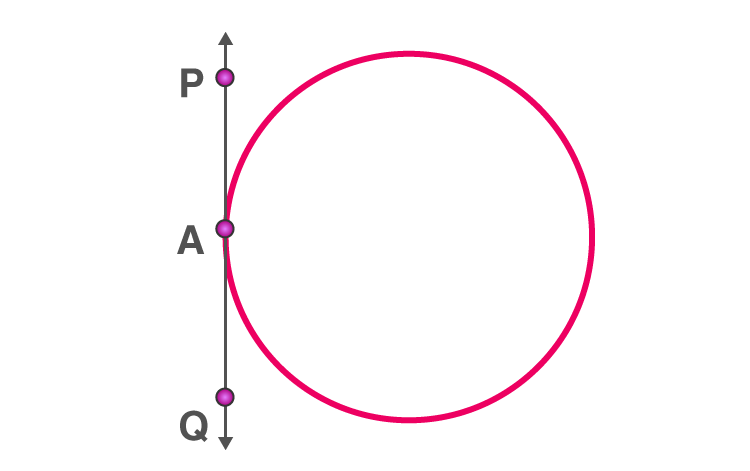
PQ is the tangent touching the circle at A
iii) When the point lies outside of the circle, there are exactly two tangents to a circle.
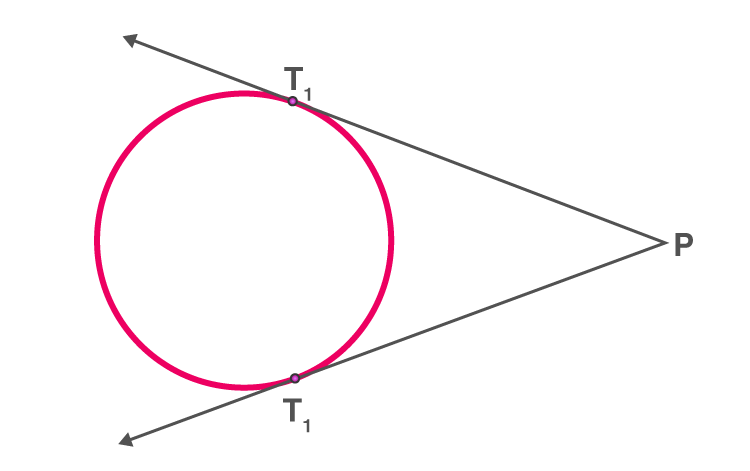
PT1 and PT2 are tangents touching the circle at T1 and T2
Drawing tangents to a circle from a point outside the circle

To construct the tangents to a circle from a point outside it.
Consider a circle with centre O and let P be the exterior point from which the tangents to be drawn.
Step 1: Join the PO and bisect it. Let M be the midpoint of PO.
Step 2: Taking M as the centre and MO(or MP) as radius, draw a circle. Let it intersect the given circle at the points Q and R.
Step 3: Join PQ and PR
Step 3:PQ and PR are the required tangents to the circle.
Drawing Tangents to a circle from a point on the circle
To draw a tangent to a circle through a point on it.
Step 1: Draw the radius of the circle through the required point.
Step 2: Draw a line perpendicular to the radius through this point. This will be tangent to the circle.
Watch The Below Video To Understand The Construction of Tangents To The Circle

To learn more about the construction of angles, perpendicular bisectors, similar triangles, and tangents to circles, etc., download BYJU’S – The Learning App today!