Continuity And Differentiability
Continuity and Differentiability is one of the most important topics which help students to understand the concepts like, continuity at a point, continuity on an interval, derivative of functions and many more. However, continuity and Differentiability of functional parameters are very difficult. Let us take an example to make this simpler:
Consider the function,
\(\left\{\begin{matrix} x+3 & if\ x \leq 0\\ x & if\ x>0 \end{matrix}\right.\)
For any point on the Real number line, this function is defined.
It can be seen that the value of the function x = 0 changes suddenly. Following the concepts of limits, we can say that;
Right-hand limit ≠ Left-hand limit.
It implies that this function is not continuous at x=0.
In simple words, we can say that a function is continuous at a point if we are able to graph it without lifting the pen.
Definition of Continuity
In Mathematically, A function is said to be continuous at a point x = a, if
\(\lim_{x\rightarrow a}\) f(x) Exists, and
\(\lim_{x\rightarrow a}\) f(x) = f(a)
It implies that if the left hand limit (L.H.L), right hand limit (R.H.L) and the value of the function at x=a exists and these parameters are equal to each other, then the function f is said to be continuous at x=a.
If the function is undefined or does not exist, then we say that the function is discontinuous.
Continuity in open interval (a, b)
f(x) will be continuous in the open interval (a,b) if at any point in the given interval the function is continuous.
Continuity in closed interval [a, b]
A function f(x) is said to be continuous in the closed interval [a,b] if it satisfies the following three conditions.
1) f(x) is be continuous in the open interval (a, b)
2) f(x) is continuous at the point a from right i.e. \(\lim\limits_{x \to a}f(x)\)=f(a)
3) f(x) is continuous at the point b from left i.e. \(\lim\limits_{x \to b}f(x)\)=f(b)
| Lets Work Out-
Example: Check whether the function \(\frac{4x^{2}-1}{2x-1}\) is continuous or not? Solution: At x=1/2, the value of denominator is 0. So the function is discontinuous at x = 1/2. |
Definition of Differentiability
f(x) is said to be differentiable at the point x = a if the derivative f ‘(a) exists at every point in its domain. It is given by
| f'(a)=\(\lim_{h\rightarrow 0}\frac{f(a+h)-f(a)}{h}\) |
For a function to be differentiable at any point x=a in its domain, it must be continuous at that particular point but vice-versa is not always true.
The derivatives of the basic trigonometric functions are;
- \(\frac{d}{dx}\)(sinx) = cosx
- \(\frac{d}{dx}\)(cosx) = −sinx
- \(\frac{d}{dx}\)(tanx) = sec2x
- \(\frac{d}{dx}\)(cotx) = –cosec2x
- \(\frac{d}{dx}\)(secx) = secx tanx
- \(\frac{d}{dx}\)(cosecx) = −cosecx cotx
| Lets Work Out-
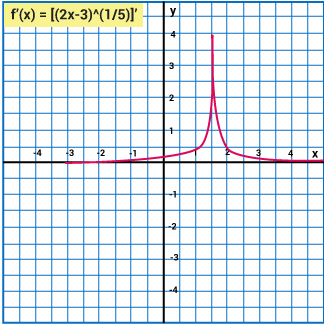
Example: Consider the function \(f(x)=(2x-3)^{\frac{1}{5}}\).Discuss its continuity and differentiability at \(x= \frac{3}{2}\). Solution: For checking the continuity, we need to check the left hand and right-hand limits and the value of the function at a point x=a. L.H.L. = \(\lim\limits_{x \to a^{-}}f(x)= \lim_{x \to \frac{3}{2}}(2x-3)^{\frac{1}{5}}\) \(= \left ( 2 \times \frac{3}{2} -3 \right )^{\frac{1}{5}}\) = 0 R.H.L. = \(\lim\limits_{x \to a^{+}}f(x)= \lim_{x \to \frac{3}{2}}(2x-3)^{\frac{1}{5}}\) \(= \left ( 2 \times \frac{3}{2} -3\right )^{\frac{1}{5}} \) = 0 L.H.L = R.H.L = f(a) = 0. Thus the function is continuous at about the point \(x= \frac{3}{2}\). Now to check differentiability at the given point, we know \(f'(a)=\lim\limits_{h \to 0}\frac{f(a+h)-f(a)}{h}\) = \(\lim\limits_{h \to 0}\frac{f(\frac{3}{2}+h)-f(\frac{3}{2})}{h}\) = \(\lim\limits_{h \to 0}\frac{\left ( [2(\frac{3}{2})+h]-3 \right )^{\frac{1}{5}}- \left ( 2(\frac{3}{2})-3 \right )^{\frac{1}{5}}}{h}\) = \(\lim\limits_{h \to 0}\frac{\left ( 3 + 2h -3 \right )^{\frac{1}{5}}- \left ( 3 -3 \right )^{\frac{1}{5}}}{h}\) = \(\lim\limits_{h \to 0}\frac{\left ( 2h \right )^{\frac{1}{5}}- 0}{h}\) = \(\lim\limits_{h \to 0}\frac{ 2^\frac{1}{5}}{h^\frac{4}{5}} = \infty\) Thus f is not differentiable at \(x= \frac{3}{2}\).
We see that even though the function is continuous but it is not differentiable. |
Learn more about limits and continuity and other topics with BYJU’S and make learning more fun.