Converse of Pythagoras Theorem
The converse of Pythagoras theorem states that “If the square of a side is equal to the sum of the square of the other two sides, then triangle must be right angle triangle”. Whereas Pythagorean theorem states that the sum of the square of two sides (legs) is equal to the square of the hypotenuse of a right-angle triangle. But, in the reverse of the Pythagorean theorem, it is said that if this relation satisfies, then triangle must be right angle triangle. So, if the sides of a triangle have length, a, b and c and satisfy given condition a2 + b2 = c2, then the triangle is a right-angle triangle.
Let us see the proof of this theorem along with examples.
Converse of Pythagoras Theorem Proof
Statement: If the length of a triangle is a, b and c and c2 = a2 + b2, then the triangle is a right-angle triangle.

Proof: Construct another triangle, △EGF, such as AC = EG = b and BC = FG = a.
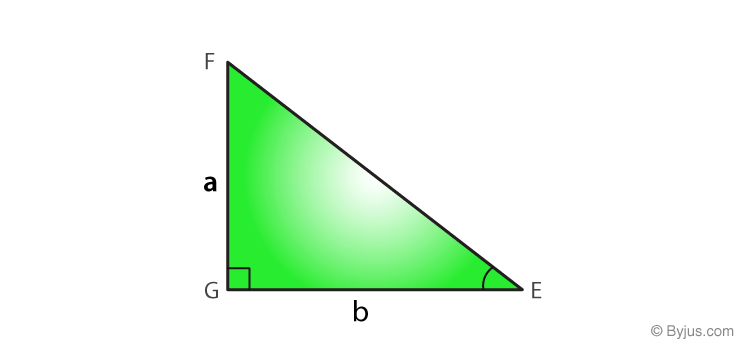
In △EGF, by Pythagoras Theorem:
EF2 = EG2 + FG2 = b2 + a2 …………(1)
In △ABC, by Pythagoras Theorem:
AB2 = AC2 + BC2 = b2 + a2 …………(2)
From equation (1) and (2), we have;
EF2 = AB2
EF = AB
⇒ △ ACB ≅ △EGF (By SSS postulate)
⇒ ∠G is right angle
Thus, △EGF is a right triangle.
Hence, we can say that the converse of Pythagorean theorem also holds.
Hence Proved.
Formula
As per the converse of the Pythagorean theorem, the formula for a right-angled triangle is given by:
| a2+b2 = c2 |
Where a, b and c are the sides of a triangle.
Applications
Basically, the converse of the Pythagoras theorem is used to find whether the measurements of a given triangle belong to the right triangle or not. If we come to know that the given sides belong to a right-angled triangle, it helps in the construction of such a triangle. Using the concept of the converse of Pythagoras theorem, one can determine if the given three sides form a Pythagorean triplet.
Converse of Pythagoras Theorem Examples
Question 1: The sides of a triangle are 5, 12 and 13. Check whether the given triangle is a right triangle or not?
Solution: Given,
a = 5
b = 12
c = 13
By using the converse of Pythagorean Theorem,
a2+b2 = c2
Or
c2 = a2+b2
Substitute the given values in the above equation,
132 = 52+122
169 = 25 + 144
169 = 169
So, the given lengths are does not satisfy the above condition.
Therefore, the given triangle is a right triangle.
Question 2: The sides of a triangle are 7, 11 and 13. Check whether the given triangle is a right triangle or not?
Solution: Given;
a = 7
b = 11
c = 13
By using the converse of Pythagorean Theorem,
c2 = a2+b2
Substitute the given values in the the above equation,
132 = 72 + 112
169 = 49 + 121
169 = 170
So, it is not satisfied with the above condition.
Therefore, the given triangle is not a right triangle.
Question 3: The sides of a triangle are 4,6 and 8. Say whether the given triangle is a right triangle or not.
Solution: Given: a = 4, b = 6, c = 8
By the converse of Pythagoras theorem
a2+b2 = c2
82 = 42 + 62
64 = 16 + 36
64 = 52
The sides of the given triangle do not satisfy the condition a2+b2 = c2.
Therefore, the given triangle is not a right triangle.