Decimals
In Mathematics, the numbers can be classified into different types, namely real numbers, natural numbers, whole numbers, rational numbers, and so on. Decimal numbers are among them. It is the standard form of representing integer and non-integer numbers. In this article, let us discuss in detail about “ Decimals”, its types, properties, and place value representation of decimal numbers with many solved examples.
Table of Contents:
What are Decimals?
In Algebra, decimals are one of the types of numbers, which has a whole number and the fractional part separated by a decimal point. The dot present between the whole number and fractions part is called the decimal point. For example, 34.5 is a decimal number.
Here, 34 is a whole number part and 5 is the fractional part.
“.” is the decimal point.
Let us discuss some other examples.
Here is the number “thirty-four and seven-tenths” written as a decimal number:
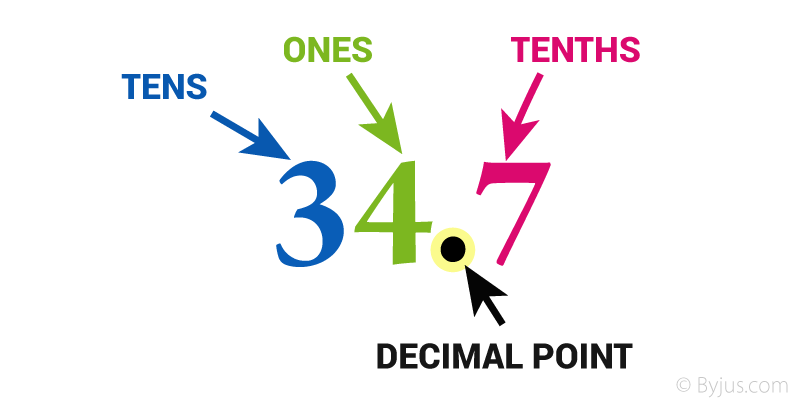
The decimal point goes between Ones and Tenths
34.7 has 3 Tens, 4 Ones and 7 Tenths
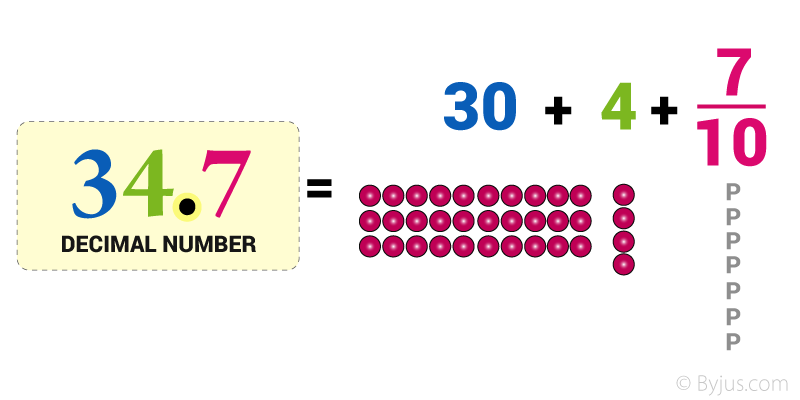
Types of Decimal Numbers
Decimal Numbers may be of different kinds, namely
Recurring Decimal Numbers (Repeating or Non-Terminating Decimals)
Example-
3.125125 (Finite)
3.121212121212….. (Infinite)
Non-Recurring Decimal Numbers (Non Repeating or Terminating Decimals):
Example:
3.2376 (Finite)
3.137654….(Infinite)
Decimal Fraction- It represents the fraction whose denominator in powers of ten.
Example:
81.75 = 8175/100
32.425 = 32425/1000
Converting the Decimal Number into Decimal Fraction:
For the decimal point place “1” in the denominator and remove the decimal point.
“1” is followed by a number of zeros equal to the number of digits following the decimal point.
For Example:
8 1 . 7 5
↓ ↓ ↓
1 0 0
81.75 = 8175/100
8 represents the power of 101 that is the tenths position.
1 represents the power of 100 that is the units position.
7 represents the power of 10-1 that is the one-tenths position.
5 represents the power of 10-2 that is the one-hundredths position.
So that is how each digit is represented by a particular power of 10 in the decimal number.
Place Value in Decimals
The place value system is used to define the position of a digit in a number which helps to determine its value. When we write specific numbers, the position of each digit is important.
Example:
For instance, let’s consider the number 456.
- The position of “6” is in One’s place, which means 6 ones (i.e. 6).
- The position of “5” is in the Ten’s place, which means 5 tens (i.e. fifty).
- The position of “4” is in the Hundred’s place, which means 4 hundred.
- As we go left, each position becomes ten times greater.
Hence, we read it as “Four hundred fifty-six”.
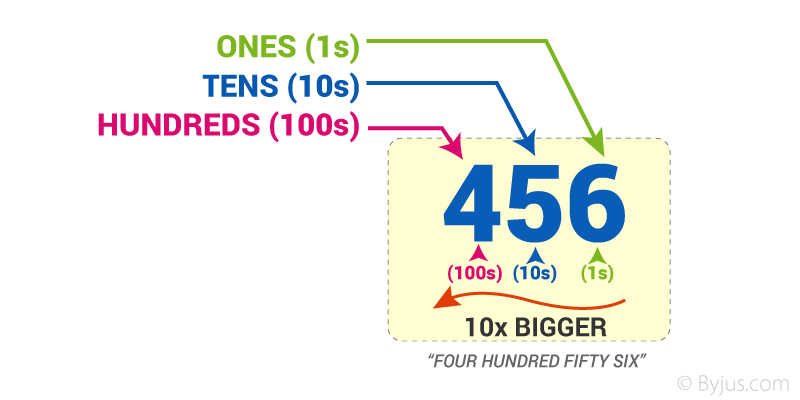
As we move left, each position is 10 times bigger!
Tens are 10 times bigger than Ones.
Hundreds are 10 times bigger than Tens.
And
Each time we move right every position becomes 10 times smaller from Hundred’s to Ten’s, to Ones
But if we continue past Ones?
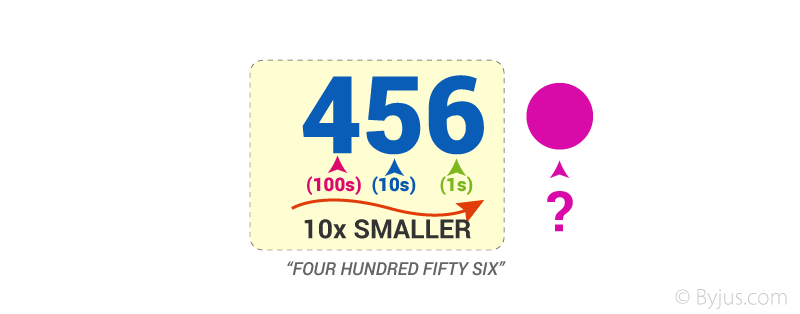
What are 10 times smaller than Ones?
\(\frac{1}{10}ths\) (Tenths) are!
Before that, we should first put a decimal point,
So we already know that where we put that decimal point.
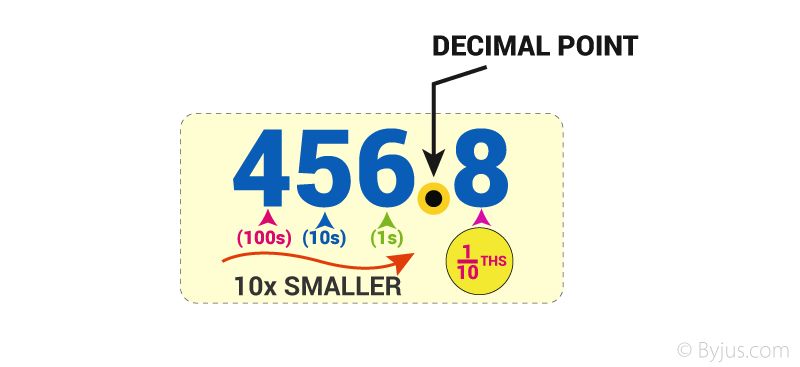
We say the above example as four hundred and fifty-six and eight-tenths but we usually just say four hundred and fifty-six point eight.
The power of 10 can be found using the following Place Value Chart:
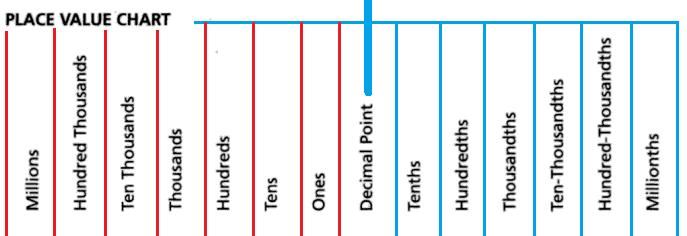
The digits to the left of the decimal point are multiplied with the positive powers of ten in increasing order from right to left.
The digits to the right of the decimal point are multiplied with the negative powers of 10 in increasing order from left to right.
Following the same example 81.75
The decimal expansion of this is :
{(8*10)+(1*1)} + {(7*0.1)+(5*0.01)}
Where each number is multiplied by its associated power of ten.
Properties of Decimals
The important properties of decimal numbers under multiplication and division operations are as follows:
- If any two decimal numbers are multiplied in any order, the product remains the same.
- If a whole number and a decimal number are multiplied in any order, the product remains the same.
- If a decimal fraction is multiplied by 1, the product is the decimal fraction itself.
- If a decimal fraction is multiplied by 0, the product is zero (0).
- If a decimal number is divided by 1, the quotient is the decimal number.
- If a decimal number is divided by the same number, the quotient is 1.
- If 0 is divided by any decimal, the quotient is 0.
- The division of a decimal number by 0 is not possible, as the reciprocal of 0 does not exist.
Arithmetic Operation on Decimals
Like integers, the arithmetic operations like addition, subtraction, multiplication, and division operation can be performed on decimal numbers. Now, let us discuss important tips while performing arithmetic operations.
Addition
While adding decimal numbers, line up the decimal points of the given numbers and add the numbers. If a decimal point is not visible (i.e., whole numbers), the decimal is behind the number.
Subtraction
Similar to the addition of decimal numbers, line up the decimal point of the given numbers, and subtract the values. To perform the arithmetic operation, use place holding zeros for our reference.
Multiplication
Multiply the given numbers like integers, as if the decimal point is not present. Find the product and count up how many numbers are present after the decimal point in both the numbers. The count represents how many numbers are required after the decimal point in the product value.
Division
To simply divide the decimal numbers, move the decimal point in the numbers such that the number becomes the whole numbers. Now, perform the division operation like the integer division.
| Related Links | |
| Decimals Word Problems | Square Root Of Decimals |
| Addition And Subtraction In Decimals | Application of Decimals in Daily Life |
Decimal to Fraction Conversion
The conversion of decimal to fraction or fraction to decimal values can be performed easily. Now, we will discuss both the conversion methods below:
Decimal to Fraction Conversion
We know the numbers after the decimal point represents the tenths, hundredths, thousandths, and so on. Thus, while converting decimal to fraction, write down the decimal numbers in the expanded form and simplify the values
For example, 0.75
The expanded form of 0.75 is 75 x (1/100) = 75/100 = 3/4.
Fraction to Decimal Conversion
To convert the fraction to the decimal, simply divide the numerator by denominator.
For example, 7/2 is a fraction. If it’s divided, we get 3.5.
Decimal Problems
Example 1:
Convert 8/10 in decimal form.
Solution:
To convert fraction to decimal, divide 8 by 10, we get the decimal form.
Thus, 8/10 = 0.8
Hence, the decimal form of 8/10 is 0.8
Example 2:
Express 1.25 in fraction form.
Solution:
The given decimal number is 1.25
The expanded form of 1.25 is
= 125 x (1/100)
= 125 /100
=5/4
Hence, the equivalent fraction for 1.25 is 5/4.
Frequently Asked Questions on Decimals
What is meant by decimals?
Decimals are the numbers, which consist of two parts namely, a whole number part and a fractional part separated by a decimal point. For example, 12.5 is a decimal number.
What are the different types of decimals?
The two different types of decimals are:
Terminating decimals (or) Non-recurring decimals
Non-terminating decimals (or) Recurring decimals
How to convert fractions to decimals?
To convert fractions to decimals, divide the numerator by the denominator value.
Write the expanded form of 74.2?
The expanded form of 74. 2 is 70 + 4 + (2/10).
When do we use decimals?
The decimal numbers are used when the problem requires more precision than the whole value. For example, while dealing with weight, money, length, and so on.
To learn more about decimals, division of decimals, and operations of converting fractions to decimals, Register with BYJU’S, and strengthen your skills.