In Mathematics, we know that the system of linear equations is defined as the set of two or more linear equations with two or more unknown variables. Solving the linear equation is finding the solutions of the unknown variables in the system of equations. There are different methods to find the solutions for the unknown variables. They are the graphical method, substitution method, elimination method, cross-multiplication method, and so on. In this article, we are going to discuss one of the methods called the “Elimination Method” in detail with the steps of solving the system of linear equations with examples.

Table of Contents:

• Solving Linear Equations by Elimination Method
• Steps in Elimination Method
• Examples
• Practice Problems
• FAQs

Solving Linear Equations by Elimination Method

The elimination method is one of the techniques to solve the system of linear equations. In this method, either add or subtract the equations to get the equation in one variable. If the coefficients of one of the variables are the same, and the sign of the coefficients are opposite, we can add the equation to eliminate the variable. Similarly, if the coefficients of one of the variables are the same, and the sign of the coefficients are the same, we can subtract the equation to get the equation in one variable.

In case, if we do not have the equation to directly add or subtract the equations to eliminate the variable, you can begin by multiplying one or both the equations by a constant value on both sides of an equation to obtain the equivalent linear system of equations and then eliminate the variable by simply adding or subtracting equations.

Also, read:

Elimination Method Steps

Step 1: Firstly, multiply both the given equations by some suitable non-zero constants to make the coefficients of any one of the variables (either x or y) numerically equal.
Step 2: After that, add or subtract one equation from the other in such a way that one variable gets eliminated. Now, if you get an equation in one variable, go to Step 3. Else;

• If we obtain a true statement including no variable, then the original pair of equations has infinitely many solutions.
• If we obtain a false statement including no variable, then the original pair of equations has no solution, i.e., it is inconsistent.

Step 3: Solve the equation in one variable (x or y) to get its value.
Step 4: Substitute this value in any of the given equations to get the value of another variable

Let us understand with a general case.

General Case: Taking a general case of two linear equations:

ax + by = c………(1)

px + qy = r……….(2)

Multiplying eq (1) by p, we get,

apx + bpy = cp ………..(3)

Similarly, on multiplying eq (2) with ‘a’, we get:

apx + aqy = ar………….(4)

As per the elimination method, the coefficient of x obtained in equation (3) and equation (4) is same.

In order to remove the variable x and get a linear equation in one variable, equation (4) is subtracted from equation (3). We get:

apx + bpy – apx – aqy = cp – ar

bpy – aqy = cp – ar

(bp – aq) y = cp – ar

y = (cp-ar)/(bp-aq)

Also, from equation (1) we get,

ax = c – by

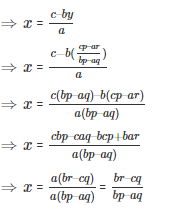
Now consider an example with the application of the elimination method.

Elimination Method Examples

Example 1:

Solve the system of equations: 2x + 7y = 10 and 3x + y = 6.

Solution:

Consider the equations:

2x + 7y = 10…………….. (1)

3x + y = 6………………… (2)

There can be two ways to solve this problem.

In a first way, multiply equation (1) by 3 and equation (2) by 2, we get,

6x + 21y = 30……………..(3)

6x + 2y = 12……………….(4)

The coefficients the x in equation (3) and equation (4) are the same i.e. 6.

Finally, subtract equation (4) from equation (3). We get-

6x + 21y – 6x – 2y = 30 – 12

⇒ 19y = 18

y =  18/19

In order to get the value of x, the value of y is substituted in equation (2),

3x + 18/19 = 6

3x = 6 – 18/19

3x = 96/19

x = 96/57 = 32/19

Alternatively, multiply equation (2) with 7,

21x + 7y = 42………….(5)

And equation (1) is 2x + 7y = 10

Subtracting equation (1) from equation (5), we get

19x = 32

x = 32/19

Substituting the value of x in Eqn. (1),

2(32/19) + 7y = 10

7y = 10 – 64/19

7y = 126/19

y = 18/19

Example 2:
The sum of a two-digit number and the number obtained by reversing the digits is 88. If the digits of the number differ by 2, find the number. How many such numbers are there?

Solution:

Let the ten’s and the unit’s digits in the first number be x and y, respectively.

So, the first number = 10x + y

After the digits have been reversed, the second number will be = x + 10y

As per the given statement;

(10x + y)+(10y + x) = 88

11x + 11y = 88

11(x + y) = 88

x + y = 8 ……….(1)

Also given, the difference between the two digits is equal to 2. Therefore;

x – y = 2 ………..(2)

or

y – x = 2 …………(3)

If we consider equation 1 and 2, then by elimination method we get,

x = 5  and y = 3

Hence, the number is 53.

If we consider equation 1 and 3, then by elimination method we get,

x = 3  and y = 5

Hence, the number is 35.

Therefore, there are two such numbers, 53 and 35.

Note: The elimination method is preferred over the substitution method when it is easy to multiply the coefficient and add or subtract the equations to eliminate one of the variables. The final aim is to form a linear equation in one variable so that it can be solved easily.

Practice Problems on Elimination Method

Solve the system of linear equations using the elimination method:

1. 2x+3y=6 and -2x+5y=10
2. 4x-9y=20 and 16x-7y=80
3. 2x-8y=10 and 3x+8y=15

To practice more problems on the solutions of pair of linear equations by elimination method, download BYJU’S  – The Learning App.