In case you have a number with many digits, it will be challenging for you to calculate the square roots and cube roots of the number by prime factorization and long division method. Hence, you will try to estimate the value of cube roots and square roots for these numbers. In prime factorization, we can find the factors of a number. Numbers such as 25, 700, 368, etc. are easy to factorize. In case, the number of digits increases, the factorization becomes difficult. In such cases estimating square root and a cube root is a good option. Let’s go through with the method of estimating square root and cube root of a number.

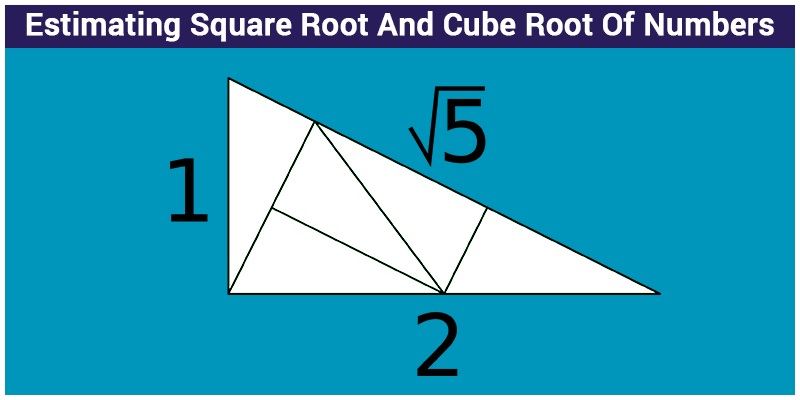
Estimating square root of a number

For estimating the number of digits in the square root of a number, we use method of bars. For example:

\( \sqrt{961} \) = 31 and \( \sqrt {1369} \) = 37

The bar is placed on pair of digits starting from the rightmost digit.

\( \overline{9} \;\overline{61}\; and\; \overline{13}\; \overline{69} \)

In both the numbers above, we have 2 bars, that means, their square root will have two digits.

In order to estimate the square root of a number, consider the following example:

The number whose square root is to be determined = 247

Since: 100 < 247 < 400, and \( \sqrt[2]{100} \) = 10 and \( \sqrt[2]{400} \) = 20.

Taking the square root we get: 10 < \( \sqrt[2]{247} \) < 20

We are not very close to the number yet.

We also know that \( 15^2 \) = 225 and \( 16^2 \) = 256, therefore 15 < \( \sqrt[2]{247} \) < 16

The number 247 is much closer to 256 than 225.

Hence \( \sqrt[2]{247} \) is approximately equal to 16.

Estimating the cube root of a cube number

If a large number is given and stated that it is a perfect cube then we can use the following method to calculate its cube root by the method of estimation.

1. Take any cube number such as 29791 whose cube root is to be determined and start making a group of three digits starting from the rightmost digit.

2. The first group will give us the unit’s digit of the required cube root. The number 791 ends in 1, therefore, the last digit will be 1 because unit’s digit is 1 only when the cube root also ends with 1.

3. Now taking the second group, it is between \(3^3\) = 27 and \(4^3\) = 64. We take the smaller value, therefore, the digit at the tenths place is 3.

The required cube root of 29791 = \( \sqrt[3]{29791} \) = 31.

To learn more about other topics download BYJU’S – The Learning App from Google Play Store and watch interactive videos. Also, take free tests to practice for exams.