Factors Of 45
Factors of 45 are the numbers which when multiplied in pairs give the result as 45. For example, multiplication 2 and 3 gives 6, which means 2 and 3 are the factors of 6. Similarly, we can find all the factors 45.
What are the Factors of 45?
Factors of 45 are the numbers, which divide the original number completely or uniformly. The numbers which give the result as 45 when multiplied together in pairs are the pair factors.
If we divide 84 with any of its factors, then the resulted quotient will be a whole number. 45, 36, 18, 60, 42, 30, 90, etc. are the composite numbers, which have more than 2 factors, unlike prime numbers. To find the factors of a number and prime factors we can use the simple multiplication method and division method.
How to Find the Factors of 45?
In this section, you will learn the method of finding the factors of 45 by the division method. In this method, we should divide 45 by natural numbers 1, 2, 3, etc., and when we get the reminder 0, the corresponding divisor and quotient are treated as factors of 45.
Let us divide 45.
45/1 = 45 × 1 + 0 {remainder = 0, so 1 and 45 are factors}
45/2 = 22 × 2 + 1 {remainder ≠ 0, so 2 and 22 are not factors}
45/3 = 15 × 3 + 0 {remainder = 0,so 3 and 15 are factors}
45/4 = 11 × 4 + 1 {remainder ≠ 0, so 2 and 22 are not factors}
45/5 = 9 × 5 + 0 {remainder = 0, so 5 and 9 are factors}
45/6 = 7 × 6 + 3 {remainder ≠ 0, so 7 and 6 are not factors}
45/7 = 6 × 7 + 3 {remainder ≠ 0, so 6 and 7 are not factors}
Here, the numbers are repeated in multiplication so we need to stop the division process.
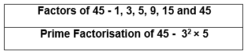
| Factors Of 45 |
| 1, 3, 5, 9, 15 and 45 |
Factors of 45 in Pair
We can find the pair factors of number 45, by multiplying two numbers in a pair to get the original number as 45, such as;
1 × 45 = 45
3 × 15 = 45
5 × 9 = 45
Therefore, the pair factors are (1, 45), (3, 15) and (5, 9).
Prime Factorization of 45
The number 45 is a composite number. Now let us take out prime factorization of 45.
- The first step is to divide the number 45 with the smallest prime factor, i.e. 2.
45 ÷ 2 = 22.5; factor cannot be a fraction.
- Now, proceed to the next prime numbers, i.e. 3.
45 ÷ 3 = 15
15 ÷ 3 = 5
- Again, if we divide 5 by 3, we get a fraction number, which is not a factor.
- Therefore, we will move to the next prime number, which is 5.
5 ÷ 5 = 1
- We have received 1 at the end and further, we cannot proceed with the division method, as ‘1’ doesn’t have any multiples. So, the prime factorization of 45 is 3 × 3 × 5 or 32 × 5, where 3 and 5 are the prime numbers.
Go through the summary of factors of 45 given in the below table:
| Factors of 45 | 1, 3, 5, 9, 15, 45 |
| Negative factors of 45 | -1, -3, -5, -9, -15, -45 |
| Positive factor pairs of 45 | (1, 45), (3, 15), (5, 9) |
| Negative factor pairs of 45 | (-1, -45), (-3, -15), (-5, -9) |
| Prime factorization of 45 | 3 × 3 × 5 (Or) 32 × 5 |
| Number of factors of 45 | 6 |
| Sum of factors of 45 | 78 |
Get Factors of more Numbers here.
Get factors of more natural numbers in the below-given links and download BYJU’S – The Learning App for a better experience of learning.
Frequently Asked Questions on Factors of 45
What are the factors of 45 in maths?
1 × 45 = 45
3 × 15 = 45
5 × 9 = 45