Hexadecimal Number System
The hexadecimal number system is a type of number system, that has a base value equal to 16. It is also pronounced sometimes as ‘hex’. Hexadecimal numbers are represented by only 16 symbols. These symbols or values are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F. Each digit represents a decimal value. For example, D is equal to base-10 13.
Hexadecimal number systems can be converted to other number systems such as binary number (base-2), octal number (base-8) and decimal number systems (base-10). The concept of the number system is widely explained in the syllabus of Class 9.
The list of 16 hexadecimal digits with their equivalent decimal, octal and binary representation is given here in the form of a table, which will help in number system conversion. This list can be used as a translator or converter also.
Hexadecimal Number System Table
Below is the table of hexadecimal number systems with equivalent values of the binary and decimal number systems.
| Decimal Numbers | 4-bit Binary Number | Hexadecimal Number |
| 0 | 0000 | 0 |
| 1 | 0001 | 1 |
| 2 | 0010 | 2 |
| 3 | 0011 | 3 |
| 4 | 0100 | 4 |
| 5 | 0101 | 5 |
| 6 | 0110 | 6 |
| 7 | 0111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
Below is the link to download the table. Students can download the PDF and learn offline too.
Download PDF – Hexadecimal Number System
Hexadecimal Number System Conversions
As we know, there are 16 digits in the hexadecimal number system, represented from 0 to 9 same as decimals, but after that, it starts with an alphabetical representation of preceding numbers such as A, B, C, D and E. Let us see the conversion of ‘hex’ into other number systems.
Hexadecimal to Decimal Conversion
Here, you will see the representation of a hexadecimal number into decimal form.
|
Hexadecimal |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Decimal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
15 |
Decimal to Hexadecimal Conversion
You have learned how to convert hexadecimal numbers to decimal numbers. Now let us find out how we can convert a decimal number into a hexadecimal number system. Follow the below steps:
- Firstly divide the number by 16
- Take the quotient and divide again by 16
- The remainder left will produce the hex value
- Repeats the steps until the quotient has become 0
Example: Convert (242)10 into hexadecimal.
Solution: Divide 242 by 16 and repeat the steps, till the quotient is left as 0.
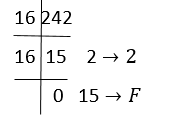
Therefore, (242)10 = (F2)16
Hexadecimal to Octal Conversion
Here, you will see the representation of a hexadecimal number into octal number form.
|
Hexadecimal |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Octal | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
17 |
Octal to Hexadecimal Conversion
To convert octal to hex, we have to first convert octal number to decimal and then decimal to hexadecimal. Let us understand it with the help of an example;
Example: Convert (121)8 into hexadecimal.
Solution: First convert 121 into decimal number.
⇒ 1 × 82 + 2 × 81 + 1 × 80
⇒ 1 × 64 + 2 × 8 + 1 × 1
⇒ 64 + 16 + 1
⇒ 81
(121)8 = 8110
Now converting 8110 into a hexadecimal number.
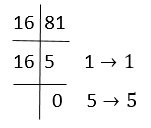
Therefore, 8110 = 5116
Hexadecimal to Binary Conversion
Here, you will see the representation of a hexadecimal number into binary form. We can use only 4 digits to represent each hexadecimal number, where each group has a distinct value from 0000 (for 0) and 1111 (for F= 15 =8 + 4 + 2 + 1).
|
Hexadecimal |
0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| Binary | 0 | 1 | 10 | 11 | 100 | 101 | 110 | 111 | 1000 | 1001 | 1010 | 1011 | 1100 | 1101 | 1110 |
1111 |
Binary to Hexadecimal Conversion
Binary to hexadecimal conversion is a simple method to do. You just have to put the values of the binary number to the relevant hexadecimal number.
Example: Convert (11100011)2 to hexadecimal.
Solution: From the table, we can write, 11100011 as E3.
Therefore, (11100011)2 = (E3)16
Facts of Hexadecimal Number System
- Out of many types of number representation techniques, the Hexadecimal number system is one having a value of base 16.
- So Hexadecimal numbers have 16 symbols or digital values, i.e 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F.
- A, B, C, D, E, F are single bit representations of 10, 11, 12, 13, 14 and 15 respectively.
- The addition of either an o prefix or an h prefix indicates Hexadecimal.
- A power of 16 is the weight of the position of every digit.
Solved Examples on Hexadecimal number system
Example 1: What is 5C6 (Hexadecimal)?
Solution: Step 1: The “5 “ is the “16 x 16” position, so that means 5 x16 x16
Step 2: The ‘C’ (12) is in the “16” position, so that means 12 x 16.
Step 3: The “6” in the “1” position so that means 6.
Answer is : 5C6 = 5 x 16 x 16 + 12 x 16 +6 = (1478 ) in Decimal.
Example 2: What is 3C5 (Hexadecimal)?
Solution: Step 1: The “3 “ is the “16 x 16” position, so that means 3 x16 x16
Step 2: The ‘C’ (12) is in the “16” position, so that means 12 x 16.
Step 3: The “5” is in the “1” position so that means 5.
Answer is : 3C5 = 3 x 16 x 16 + 12 x 16 + 5 = (965) in Decimal.
Example 3: What is 7B5 (Hexadecimal)?
Solution: Step 1: The “7 “ is the “16 x 16” position, so that means 7 x16 x16
Step 2: The ‘B’ (11) is in the “11” position, so that means 11 x 16.
Step 3: The 5” in the “1” position so that means 5.
Answer is : 7B5 = 7 x 16 x 16 + 11 x 16 +5 = (1973) in Decimal.
Example 4: What is 2E8 (Hexadecimal)?
Solution: Step 1: The “2 “ is the “16 x 16” position, so that means 2 x16 x16
Step 2: The ‘E’ (14) is in the “16” position, so that means 14 x 16.
Step 3: The “2” is in the “1” position so that means 2.
Answer is : 2E8 = 2 x 16 x 16 + 14 x 16 +8 = (744) in Decimal.
Example 5: What is 4F8 (Hexadecimal)?
Solution: Step 1: The “4 “ is the “16 x 16” position, so that means 4 x16 x16
Step 2: The ‘F’ (15) is in the “16” position, so that means 15 x 16.
Step 3: The “8” is in the “1” position, which means 8.
Answer is : 4F8 = 4 x16 x 16 + 15 x 16 +8 = (1272) in Decimal.
Practice Questions
- What is 5D16 in decimal number?
- Convert decimal number 21 into a hexadecimal number.
- What is 01101112 in hexadecimal?
Related Articles
- Number System Conversion
- Binary Number System
- Octal Number System
- Hexadecimal Calculator
- Number System For Class
- Important Questions Class 9 Maths Chapter 1 Number System
Keep visiting BYJU’S and Subscribe to our YouTube channel for learning number system and other mathematical topics in a fun and engaging way.