A fraction is defined as a part of a whole or, more commonly, any number of equal parts. Sometimes we want to add or subtract two fractions to find out the total number. This activity is called Addition and Subtraction of Fractions. For example, Malini ate 1 ½ roties for lunch and 2 ½ roties for dinner. What is the total number of roties Malini ate? In the above example, it is necessary to add the fractions. How do add or subtract fractions? What are the steps involved to add or subtract fractions? Let us take an overview of the Addition and Subtraction of Fractions.

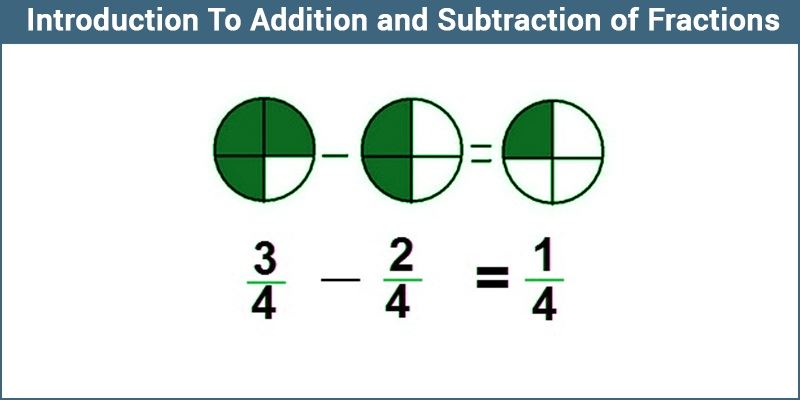
Addition and Subtraction of Fraction Methods

All fractions cannot be added or subtracted easily. The following methods are available to add or subtract fractions.

1. Add or subtract fraction with the same denominator
2. Add or subtract fraction with different denominator
3. Add or subtract mixed number fraction

Addition or Subtraction of Fractions with the Same Denominator

In this method, the addition or subtraction of a fraction is very easy. Because the denominators of the two fractions are the same.

Example: ²/₄ + ³/₄ = ?

In the above fractions, the denominators are the same.

²/₄ =

 ³/₄  =

In the above fractions, the box is divided into four parts. For ²/₄  and ³/₄, take numerator parts respectively out of 4 equal parts.

The steps involved in adding fractions with the same denominators are given below:

Step 1: Check the given fractions, if denominators are the same or not.

Step 2: If denominators are the same, take the numerators of two fractions and add or subtract them.

Step 3: Give a final answer with denominator.

Example 1: 5/8 + 2/8 = ?

Step 1: Denominators are the same.

Step 2: Take the numerators 5 and 2 respectively and add them.

 = (5+2)/8

Step 3: Give the final answer.

= 7/8

Example 2: 5/8 – 2/8 =?

Step 1: Denominators are the same.

Step 2: Take the numerators 5 and 2 respectively and subtract the smaller from the bigger numerator.

 = (5-2)/8

Step 3: Give the final answer.

= ⁷/₈

Addition or Subtraction of Fractions with the Different Denominator

In this method, the denominators are not the same in two fractions. Thus, the numerators and denominators are different in the two fractions. So we need to make the denominators equal. 

Let us add two fractions, 3/8 and 5/12.

In the above fractions, numerators and denominators are different. Let’s have a look at the stepwise solution for the addition of two fractions 3/8 and 5/12.

Step 1: Take LCM for denominators of above fractions. i.e. 8 and 12 respectively.

(LCM is the smallest number which is used as a common multiple of two numbers)

24 is a common multiple for 8 and 12.

Step 2: Convert denominators 8 and 12 into 24.

For 3/8, multiply numerator and denominator by 3 = 3/8 x3/3 = 9/24

For 5/12, multiply numerator and denominator by 2 = 5/12x 2/2 = 10/24

Step 3: Now, the denominators of the two fractions are the same.

9/24, 10/24

Step 4: Take the numerators 9 and 10 respectively and add them.

= (9+10)/24

Step 5: Give a final answer

= 19/24

Similar procedure can be followed to subtract the fractions with different denominators.

Example: 3/8 – 5/12 =?

Solution: 

Step 1: Denominators are different. So, take the Least Common Multiple (LCM).

24 is a common multiple of 8 and 12.

Step 2: Make the denominators equal by multiplying 3/3 with ⅜ and multiplying 2/2 with 5/12.

3/8 => 3/8 x3/3 = 9/24

5/12 => 5/12x 2/2 = 10/24

Step 3: Take the numerators and subtract.

3/8 – 5/12  = 9/24 – 10/24

= (9-10)/24 (subtract the smaller numerator from the bigger)

Step 4: Answer   = ^-1/₂₄

Addition and Subtraction of Mixed Fractions

A mixed fraction is defined as a fraction and a whole number combined into one “mixed” number.

Depending on the denominator, two following methods are available for adding or subtracting a mixed fraction.

1. If the same denominators are present in the mixed fraction.
2. If different denominators are present in the mixed fraction.

Click here to learn more about mixed fractions.

Addition or Subtraction of Mixed Fractions with the Same Denominator

In this method, the mixed fraction consists of the same denominators. The following steps are involved to add or subtract the mixed fraction.

Step 1: Add the whole number of two fractions separately.

Step 2: Add the fractions separately.

Step 3: Combine the whole number and the fraction both

Step 3: Convert improper fraction into a mixed fraction.

Example:  3 ²/₅ + 1 ⁴/₅ = ?

Step 1: Add the whole number of two fraction separately

= 3+1 = 4 — (1)

Step 2: Add the fractions separately

= ²/₅ + ⁴/₅ = ⁶/₅ —– (2)

Step 3: Combine the both equation (1) and (2)

= 4 ⁶/₅ —— (3)

In 4 ⁶/₅, ⁶/₅ is an improper fraction. So, convert into proper mixed fraction.

Equation (2) —–> ⁶/₅ = 1 ¹/₅ —– (3)

Step 4: Now, add equation (1) and (3)

4 + 1 ¹/₅ = 5 ¹/₅

Answer = 5 ¹/₅

Alternative Method:

In this method, the step is to convert the given mixed fraction into improper fraction and then we can perform the addition or subtraction.

Click here to convert the mixed fraction to improper fraction online.

The steps involved in this method are:

• Convert the mixed fractions to improper fractions.
• Check the denominators whether they are equal.
• Now, take the denominator as common and add or subtract (as per the given) the numerators.
• Finally, simplify the answer.

Thus, the above example can be solved as:

3 2/5 + 1 4/5 = ?

3 ⅖ = 17/5

1 ⅘ = 9/5

Now, 3 2/5 + 1 4/5 = 17/5 + 9/5

= (17 + 9)/5

= 26/5

Or

= 5 1/5

Addition or Subtraction of Mixed Fractions with the Different Denominator

In this method, the mixed fraction consists of different denominators. The following steps are involved to add or subtract the mixed fraction.

Example: 6 ³/₄ + 3 ⁵/₈ = ?

Solution: In the above-mixed fractions, the denominators are different. So we need to make the denominators the same.

Step 1: Take LCM for denominators of above fractions. i.e. 4 and 8 respectively.

(LCM is the smallest number which is used as a common multiple of two numbers)

8 is a common multiple for 4 and 8.

Step 2: Convert denominators 4 and 8 into 8.

In ³/₄, multiply numerator and denominator by 2 = ³/₄ x²/₂ = ⁶/₈

In ⁵/₈, multiply numerator and denominator by 1 = ⁵/₈x ¹/₁ = ⁵/₈

(Note: We must do to the numerator what we do to the denominator)

Now, denominators are the same in the mixed fraction

6 ³/₄ + 3 ⁵/₈  = 6 ⁶/₈ + 3 ⁵/₈

Step 3: Add the whole number of two fractions separately

= 6+3 = 9 ———— (1)

Step 4: Add the fractions separately

= ⁶/₈ + ⁵/₈= ¹¹/₈ —– (2)

¹¹/₈ is an improper fraction. So, convert into a proper fraction.

¹¹/₈ = 1 ³/₈ ————(3)

Step 5: Combine both equation (1) and (3)

9+ 1 ³/₈ = 10 ³/₈

Answer: 10 ³/₈

Alternative Method:

The steps involved in this method are:

• Convert the mixed fractions to improper fractions.
• Check the denominators whether they are equal if not make them equal.
• Now, take the denominator as common and add or subtract (as per the given) the numerators.
• Finally, simplify the answer.

Thus, the above example can be solved as:

6 ¾ + 3 ⅝ = ?

6 ¾ = 27/4

3 ⅝ = 29/8

The LCM of 4 and 8 is 8.

Now, make the denominators equal.

(27/4) × (2/2) = 54/8

29/8 × (1/1) = 29/8 

Now, 

6 ¾ + 3 ⅝ = (54/8) + (29/8)

= (54 + 29)/8

= 83/8

= 10 ⅜

Similarly, we can subtract the mixed fractions.

Suppose 6 ¾ –  3 ⅝ = (54/8) – (29/8) = (54 – 29)/8 = 25/8 = 3 1/8

Practice Problems on Addition and Subtraction of Fractions

1. Find the sum of 3/7 and 5/8.
2. Subtract 5 ¼ from 6 2/7.
3. Add 6/9, 2/9 and 11/9.
4. Subtract 26/49 from 16/42.

We have thus seen this basic introduction of Addition and Subtraction of Fractions. For the complete understanding of the topic please visit our site or download the BYJU’S – The learning app.