Inverse Cosine
Inverse Cosine is one of the Trigonometric functions. It is also called the arccosine function. Each trigonometric function has an inverse function of it, whether it is sine, cosine, tangent, secant, cosecant and cotangent. These functions are also widely used, apart from the trigonometric formulas, to solve many problems in Maths.
Inverse functions are also called as Arc Functions because they give the length of the arc for a given value of trigonometric functions. They are usually written as arcsin(x), arccos(x), arctan(x), etc. Here we will discuss cosine’s inverse function rules and formulas. Also, you can check the other inverse functions, their formulas and find calculators to evaluate the values.
What is Inverse Cosine?
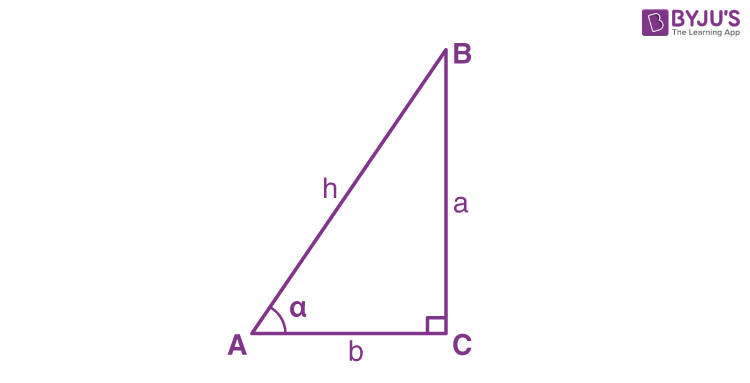
In a right-angled triangle, the cosine function is defined as the ratio of the length of base or adjacent side of the triangle(adjacent to angle) to that of the hypotenuse(the longest side) of the triangle. The Inverse Cosine function is the inverse of the Cosine function and is used to obtain the value of angles for a right-angled triangle.
What is Arccosine?
Inverse cosine is also known as arccosine. It is the inverse of cos function. Also, sometimes abbreviated as ‘arccos’. It is used to measure the unknown angle when the length of two sides of the right triangle are known.
The other inverse trig functions are also named in a similar way as per given in the below table.
| Function | Inverse Trig Function |
| sine | arcsine |
| cosine | arccosine |
| tangent | arctangent |
| secant | arcsecant |
| cosecant | arccosecant |
| cotangent | arccotangent |
Properties of Inverse Cosine
- cos-1x = sec-1x, x ≥ 1 or x ≤ – 1
- cos-1 (–x) = π – cos-1 x, x ∈ [– 1, 1]
- sin-1 x + cos-1 x = π/2, x ∈ [– 1, 1]
Inverse Cosine Function Graph
The inverse of the cosine function is also called as “Arc Function” and is denoted as Arccos or Arccosine (acos). The graph of Arccosine function is given below;
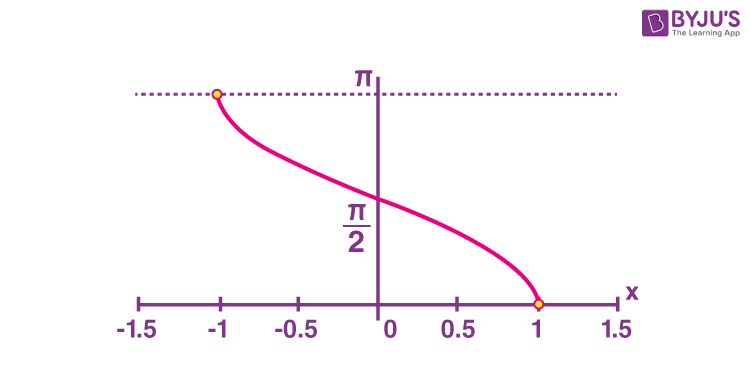
Where y=cos-1 x(arccosine of x)
Domain of Inverse Cosine Function
The domain and range of arccosine function is denoted as;
Domain: −1 ≤ x ≤ 1
Range: 0 ≤ y ≤ π
Similarly, we can define other arc functions like;
Arcsine functions(inverse of sine function)
y = sin-1 x
Arctangent function(inverse of tangent function)
y = tan-1 x
Arccotangent function(inverse of cotangent function)
y = cot-1 x
Arcsecant function(inverse of secant function)
y = sec-1 x
And Arccosecant function(inverse of cosecant function)
y = cosec-1 x
Inverse Cosine Formula
As we know, the formula for cosine function, according to the above-given diagram is,
Cos α = Base/Hypotenuse
I.e. Cos α =b/h
Therefore, the inverse cosine formula becomes;
| cos-1(Base/Hypotenuse) = α |
Hence, we get the value for the angle α here.
Inverse Cosine Solved Examples
Problem 1: Let the value of the base is √3 and the hypotenuse is 2. Find the value of angle α?
Solution: By the inverse cos formula we know,
α = cos-1(Base/Hypotenuse)
α = cos-1(√3 /2)
Therefore, α = 30°
Problem 2: Find angle α, if the value of the base or adjacent side is 1 and the value of the hypotenuse is 2.
Solution: We know, cos α=Base/Hypotenuse=b/h
And cos-1(Base/Hypotenuse) = α
cos-1(1/2)= α
Therefore, α = 60°
Learn more about trigonometric functions by downloading BYJU’S- The Learning App.