The laws of tangent (Law of Tan) describes the relation between difference and sum of sides of a right triangle and tangents of half of the difference and sum of corresponding angles. It represents the relationship between the tangent of two angles of a triangle and the length of the opposite sides. The law of tangents is also applied to a non-right triangle and it is equally as powerful like the law of sines and the law of cosines. It can be used to find the remaining parts of a triangle if two angles and one side or two sides and one angle are given which are referred to as side-angle-side(SAS) and angle-side-angle(ASA), from the congruence of triangles concept.

To understand the law of tangents in a better way, you need some pieces of information for a general triangle even it may or may not be a triangle. The four cases involved are:

• Two sides and one opposite angle
• One side and two angles
• Three Sides
• Two sides and the angle between them

Formulas For Laws Of Tangents

Let us assume a right triangle ABC in which sides opposite to \(\angle A,\angle B, and \angle C\) are a, b and c respectively. Then, according to the laws of tangent, we have the following three relations :

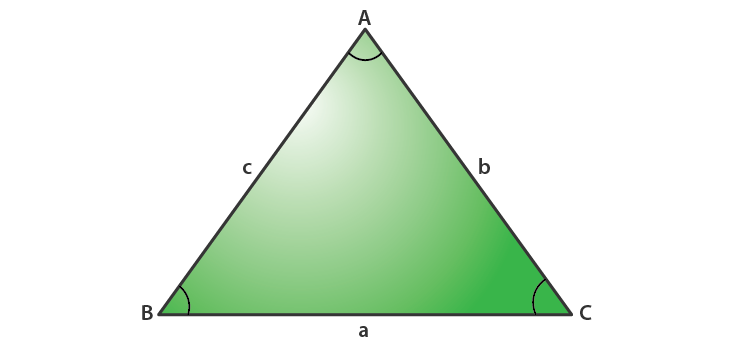
\(\frac{a-b}{a+b}=\frac{\tan (\frac{A-B}{2})}{tan(\frac{A+B}{2})}\) ….(1)

Similarly for other sides,

\(\frac{b-c}{b+c}=\frac{\tan (\frac{B-C}{2})}{tan(\frac{B+C}{2})}\) …..(2)

\(\frac{c-a}{c+a}=\frac{\tan (\frac{C-A}{2})}{tan(\frac{C+A}{2})}\) …..(3)

Since tan (-θ)= -tan θ for any angle θ, we can switch the order of letters in the above law of tangents formulas and can be rewritten as:

\(\frac{b-a}{b+a}=\frac{\tan (\frac{B-A}{2})}{tan(\frac{B+A}{2})}\) ….(4)

Similarly for other sides,

\(\frac{c-b}{c+b}=\frac{\tan (\frac{C-B}{2})}{tan(\frac{C+B}{2})}\) …..(5)

\(\frac{a-c}{a+c}=\frac{\tan (\frac{A-C}{2})}{tan(\frac{A+C}{2})}\) …..(6)

The formulas (1), (2), and (3) are used when a>b, b>c, and c>a, and the formulas (4), (5) and (6) are used when b>a, c>b and a>c.

Laws Of Tangent Proof

To Prove: \(\frac{a-b}{a+b}=\frac{\tan (\frac{A-B}{2})}{tan(\frac{A+B}{2})}\)

Proof:From the law of Sine,

\(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)

Use first and second relation,

\(\frac{a}{\sin A}=\frac{b}{\sin B}=k\) , (say)

a = k sin A and b = k sin B

From this,

a – b = k (sin A – sin B)

a + b = k (sin A + sin B)

So, we get

\(\frac{a-b}{a+b}=\frac{\sin A-\sin B}{\sin A+\sin B}\) ………(1)

Identity Formulas for Sine are:

\(\sin A-\sin B={2\cos \frac{ A+B}{2}}{\sin \frac{A-B}{2}}\\ \sin A+\sin B={2\sin \frac{ A+B}{2}}{\cos \frac{A-B}{2}}\)

Substitute those formulas in equation (1),we get

\(\frac{a-b}{a+b}=\frac{{2\cos \frac{ A+B}{2}}{\sin \frac{A-B}{2}} }{{2\sin \frac{ A+B}{2}}{\cos \frac{A-B}{2}}}=\frac{\tan \frac{A-B}{2}}{\tan \frac{A+B}{2}}\)

Hence Proved.

Practice problem

Question :

Solve the triangle \(\bigtriangleup ABC\) given a=5,b=3 and ∠C=96° and find the value of A – B.

Solution :

We know that,

∠A + ∠B + ∠C = 180°

∠A + ∠B=  180°- ∠C  = 180° – 96° = 84°

By law of tangents,

for a triangle ABC with sides a, b and c respective to the angles A , B and C is given by,

\(\frac{a-b}{a+b}=\frac{\tan (\frac{A-B}{2})}{tan(\frac{A+B}{2})}\)

Therefore,

\(\Rightarrow \frac{5-3}{5+3}=\frac{\tan \frac{1}{2}(A-B)}{\tan \frac{1}{2}(84^{\circ})}\) \(\Rightarrow \tan \frac{1}{2}(A-B)=\frac{2}{8}\tan 42^{\circ}=0.2251\) \(\Rightarrow \frac{1}{2}(A-B)=12.7^{\circ}\)

A – B = 25.4°

Register with BYJU’S -The Learning App to get more information about maths-related articles and start practice with the problems.