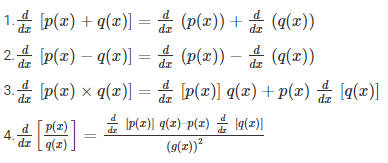Limits and derivatives are extremely crucial concepts in Maths whose application is not only limited to Maths but are also present in other subjects like physics. In this article, the complete concepts of limits and derivatives along with their properties, and formulas are discussed. This concept is widely explained in the class 11 syllabus.  We will cover the important formulas, properties and examples questions to understand the concept of limits as well as derivatives in detail.
Table of Contents:

• Introduction to Limits and Derivatives
• Limits of a Function
  • Limit Representation
  • Limits Formula
  • Properties of Limits
• Derivatives of a Function
  • Formula
  • Properties of Derivatives
• Limits and Derivatives Examples
• Practice Problems
• FAQs

Limits and Derivatives Introduction

Sir Issac Newton, based on his concepts of rate and change, set forth the basic laws of differential calculus and integral calculus came forth as the reverse process. The basics of differentiation and calculus serve as the foundation for advanced mathematics, modern physics and various other branches of modern sciences and engineering. Limits and derivatives class 11 serve as the entry point to calculus for CBSE students.

Limits of a Function

In Mathematics, a limit is defined as a value that a function approaches as the input, and it produces some value. Limits are important in calculus and mathematical analysis and used to define integrals, derivatives, and continuity.

Limits Representation

To express the limit of a function, we represent it as:

Limits Formula

The following are the important limits formulas:

Limits of Important Trigonometric Functions:

• \(\lim_{x \to 0} sin x = 0\)
• \(\lim_{x \to 0} cos x = 1\)
• \(\lim_{x \to 0} \frac{1-cos x}{x} = 0\)
• \(\lim_{x \to 0} \frac{sin^{-1}x}{x} = 1\)
• \(\lim_{x \to 0} \frac{tan^{-1} x}{x} = 1\)
• \(\lim_{x \to 0} \frac{sin x}{x} = 1\)
• \(\lim_{x \to 0} \frac{tan x}{x} = 1\)

L’hospital’s Rule:

\(\lim_{x \to a} \frac{f(x)}{g(x)} = \frac{f'(a)}{g'(a)}\), if \(\lim_{x \to a} \frac{f(x)}{g(x)}\) gives the form 0/0.

Where, f(a)=0 and g(a)=0.

Limits of Exponential and Log Functions:

• \(\lim_{x \to 0} e^{x}=1\)
• \(\lim_{x \to 0} \frac{e^{x}-1}{x}=1\)
• \(\lim_{x \to \infty } \left ( 1+\frac{1}{x} \right )^{x}=e\)
• \(\lim_{x \to \infty } \left ( 1+\frac{a}{x} \right )^{x}=e^{a}\)
• \(\lim_{x \to 0} (1+x)^{\frac{1}{x}}=e\)
• \(\lim_{x \to 0} \frac{a^{x}-1}{x}=log_{e}a\)
• \(\lim_{x \to 0} \frac{log(1+x)}{x}=1\)

Xⁿ Formula:

\(\lim_{x \to a} \frac{x^{n}-a^{n}}{x-a}= n(a)^{n-1}\)

How to Check If Limit Exists?

To check whether the limit exists for the function f(x) at x=a,

We have to check, if

Left hand side limit = Right Hand side limit = f(A)

(i.e.), \(\lim_{x \to a^{-}} f(x) = \lim_{x \to a^{+}} f(x)= f(a)\)

Properties of Limits

Let p and q be two functions and a be a value such that \(\displaystyle{\lim_{x \to a}p(x)}\) and \(\displaystyle{\lim_{x \to a}q(x)}\) exists.

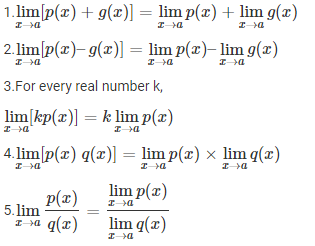
Also, check out the limit formula page here to learn more about it in detail. The formula is explained using solved examples which can help to understand the problem-solving strategies.

Derivatives of a Function

A derivative refers to the instantaneous rate of change of a quantity with respect to the other. It helps to investigate the moment by moment nature of an amount. The derivative of a function is represented in the below-given formula.

Derivative Formula

For the function f, its derivative is said to be f'(x) given the equation above exists. Check out all the derivative formulas here related to trigonometric functions, inverse functions, hyperbolic functions, etc.

Properties of Derivatives

Some of the important properties of derivatives are given below:

Limits and Derivatives Examples

Example 1:

Find \(\lim_{x\rightarrow3}x+3\)

Solution:

\(\lim_{x\rightarrow3}x+3=3+3=6\)

Example 2:

Find the derivative of the sin x at x = 0.

Solution:

Say, f(x) = sin x

then, f'(0) = lim_h→0 [f(0+h) – f(0)]/h

=  lim_h→0 [sin(0+h) – sin(0)]/h

=  lim_h→0 [sin h]/h

= 1

Example 3: 

Compute \(\lim_{x \to 0} \frac{sin(2+x) – sin (2-x)}{x}\)

Solution:

Given:

\(\lim_{x \to 0} \frac{sin(2+x) – sin (2-x)}{x}\) 

= \(\lim_{x \to 0} \frac{2cos\frac{(2+x+2-x)}{2}sin \frac{2+x-2+x}{2}}{x}\)

=\(\lim_{x \to 0} \frac{2cos2 sinx}{x}\)

= \(2cos 2\lim_{x \to 0} \frac{sinx}{x}\)

= 2 cos 2 (1)  (As, \(\lim_{x \to 0} \frac{sinx}{x} = 1\))

Hence, \(\lim_{x \to 0} \frac{sin(2+x) – sin (2-x)}{x} = 2 cos 2\)

Practice Questions From Limits and Derivatives

1. Evaluate \(\lim_{x\rightarrow3}\frac{x^{2}-9}{x-3}\)
2. \(\lim_{x\rightarrow1}\frac{x^{2}+2x+5}{x^{2}+1}\)
3. \(\lim_{x\rightarrow0}\frac{sin(a+x)-sin(a-x)}{x}\)
4. Calculate \(\frac{dy}{dx}\;at\;x=1\;if\;y=\sqrt{x}+\frac{1}{\sqrt{x}}\)
5. Find the derivative of y = 1 – x² + x – 3x⁴

Keep visiting BYJU’S to get more such Maths lessons along with notes, preparation tips, and other study materials like syllabus, sample papers, and revision notes.