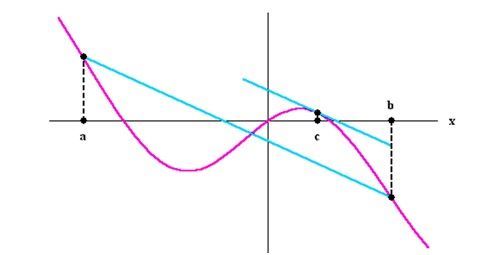
Mean Value Theorem
The Mean Value Theorem is considered to be among the crucial tools in Calculus. This theorem is very useful in analyzing the behaviour of the functions. As per this theorem, if f is a continuous function on the closed interval [a,b] (Continuous Integration) and it can be differentiated in open interval (a,b), then there exist a point c in interval (a,b), such as;
\(f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}\)Let us go through the proof of this theorem along with the applications for integrals and derivatives.
Table of Contents:
- Statement
- Proof
- Mean Value Theorem for Integrals
- Mean Value Theorem for Derivatives
- Applications
- Example
What is Mean Value Theorem?
According to the theorem, if f(x) is defined and is continuous on the interval [a,b] and can be differentiated on (a,b), then we have at least one value c in the interval (a,b) wherein a<c<b , such that
\(f’\left ( c \right )=\frac{f\left ( b \right )-f\left ( a \right )}{b-a}\)
Rolle’s Theorem is a special case where f(a) = f(b). Here, we have f’(c) = 0. If put differently, there is a point at the interval (a,b) that consists of a horizontal tangent. The Mean Value Theorem can also be stated based on slopes.
\(\frac{f\left ( b \right )-f\left ( a \right )}{b-a}\)
Mean Value Theorem proof
The mean value theorem can be proved using the slope of the line. The value is a slope of line that passes through (a,f(a)) and (b,f(b)). Therefore, the conclude the Mean Value Theorem, it states that there is a point ‘c’ where the line that is tangential is parallel to the line that passes through (a,f(a)) and (b,f(b)).
Mean Value Theorem for Integrals
The mean value theorem for integrals is the direct consequence of the first fundamental theorem of calculus and the mean value theorem. This theorem states that if “f” is continuous on the closed bounded interval, say [a, b], then there exists at least one number in c in (a, b), such that
\(f(c) = \frac{1}{b-a}\int_{a}^{b}f(t)dt\)
Mean Value Theorem for Derivatives
Suppose f is a continuous, real-valued function, described on an arbitrary interval (I) of the real line. If the derivative of function f at each interior point of I exists and is equal to zero, then f is constant in the interior.
Proof: Let (a, b) be an arbitrary open interval in I. By the mean value theorem, there exists a point c in (a,b) such that;
\(0=f^{\prime}(c)=\frac{f(b)-f(a)}{b-a}\)This indicates that f(a) = f(b). Thus, f is continuous on the interior of I.
Mean Value Theorem Applications
There are several applications of mean value theorem. This theorem is applied in:
- Leibniz’s rule
- L’Hospital’s rule
- The symmetry of second derivatives
- If f: (a, b) → R is differentiable and f ‘ (x) = 0 for all x ∈ (a, b), then “f” is constant
- If f is an open set in Rn and f : A → Rm is a function with continuous partial derivatives, then the function “f” is differentiable
Mean Value Theorem Example
Let f(x) = 1/x, a = -1 and b=1.
We know, f(b) – f(a)/b-a
= 2/2 = 1
While, for any cϵ (-1, 1), not equal to zero, we have
f’(c) = -1/c2 ≠ 1
Therefore, the equation f’(c) = f(b) – f(a) / b – a doesn’t have any solution in c. But this does not change the Mean Value Theorem because f(x) is not continuous on [-1,1].
For more Maths theorems, register with BYJU’S – The Learning App and download the app to explore interesting videos.