Natural Numbers and Whole Numbers
In Mathematics, the Number system consists of all types of numbers used to perform various calculations. These numbers include natural numbers and whole numbers, prime numbers and composite numbers, integers, real numbers and imaginary numbers etc.
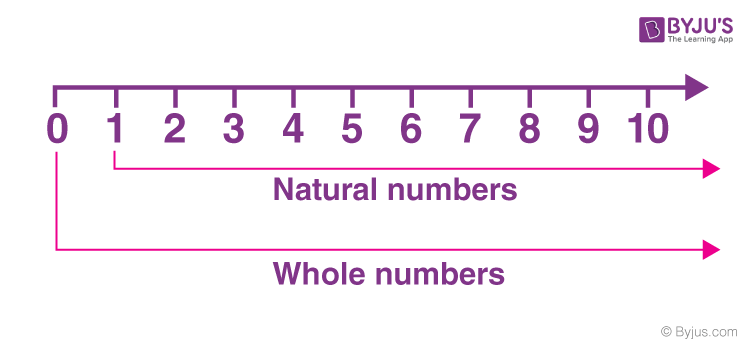
Natural numbers and whole numbers, we have studied since our primary classes. Natural numbers are set of positive integers, whereas natural numbers and zero(0) are called whole numbers, where zero is an undefined identity that produces a null result. Zero is the primary difference between natural and whole numbers.
Natural and whole numbers in Maths have equal importance. Suppose, if we have to count for a number of objects, then we start from numbers 1,2,3,4 and so on, but once these objects are all vanished, what count it gives is zero. There is a further classification of natural numbers. Let us have a look at the brief about both natural numbers and whole numbers in this article.
Natural Numbers
Natural numbers are the set of positive integers, from 1 to ∞ , but it doesn’t include fractional and decimal numbers. They are also known as counting numbers.
Natural Numbers: 1, 2, 3, 4, 5, 6,…….,∞
Types of natural numbers:
- Prime Numbers
- Even and Odd numbers
- Composite numbers
- Co-prime numbers
- Perfect numbers
Learn more about natural numbers here.
Whole Numbers
Whole numbers are also a set of positive integers, including 0, i.e. from 0 to ∞. They also don’t include fractional and decimal parts.
Whole Numbers: 0, 1, 2, 3, 4, 5, 6,…….,∞
To understand more about whole numbers, visit here.
| Read more: |
Natural Numbers and Whole Numbers Properties
Both natural numbers and whole numbers follow several properties under addition, subtraction, multiplication and division. They are:
However, these properties can be defined based on the operator are defined below:
Addition Property
When two natural numbers are added, it results in a natural number only.
Eg: 34 + 45 = 79
When two whole numbers are added, it results in the whole number only.
Eg: 6 + 0 = 6
Subtraction Property
When two natural numbers are subtracted, it may or may not result in a natural number.
Eg: 5 – 2 = 3 is natural number
But 2 – 5 = -3 is not a natural number
The same is the condition for whole numbers. If two whole numbers are subtracted, it is not necessary to result in the whole number.
Multiplication Property
When two natural numbers or whole numbers are multiplied, then it always results in natural numbers and whole numbers, respectively.
Eg: 2 X 6 = 12 is a natural number
4 X 0 = is a whole number, where 4 and 0 are also whole numbers.
Division Property
Division of two natural numbers and whole numbers may or may not result in natural and whole numbers, respectively. If the result is in fraction or decimal, they are not considered as natural and whole numbers.
E.g.: 4/2 = 2 is natural, as well as the whole number
But 5/2 = 2.5 is neither a natural nor a whole number.
Additive identity
The number 0 is called the additive identity for both natural and whole numbers. Thus, the addition of any natural number or whole number with 0 gives the number itself.
E.g. 4 + 0 = 4
Here, 4 is a natural number as well as a whole number.
Multiplicative identity
1 is called the multiplicative identity for both natural numbers and whole numbers. Multiplying any natural number and whole number by 1 results in the same natural number or whole number.
E.g. 9 × 1 = 9
0 × 1 = 0
Solved Examples
Example 1: Which of the following is not a natural number?
- 1
- 0
- 7
- 100
Solution:
Correct option: (b)
Natural numbers: 1, 2, 3, 4,…, 100,…
Whole numbers: 0, 1, 2, 3,…
Thus, 0 is not a natural number.
Example 2: Choose the whole numbers from the following.
9, -3, 0, 28, ½, -1, 14, 9/10
Solution:
Whole numbers include all the positive integers and 0.
So, the whole numbers from the given list are: 9, 0, 28, 14
To learn more about numbers, download BYJU’S – The Learning App today!