Before talking about lines that are parallel to the same line, let us recall what parallel lines are. Non-intersecting or parallel lines are the lines that do not intersect each other. They are always at the same distance from one another. Hence, they never meet. Say you are given a line A that is parallel to a line. There is another line B which is parallel to the same line. Does this imply that lines A and B are parallel to each other? We will discuss it in this article.

Lines Parallel to the Same Line

To check whether lines parallel to the same line are parallel or not, let us take an example. In the following figure, we are given that line a and line c are parallel to line b.

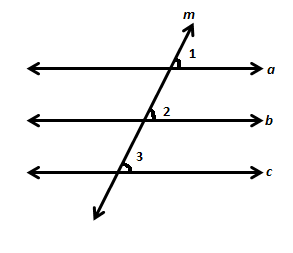
Since a || b, so ∠1 = ∠2                                 (Corresponding angles axiom)

Since c || b, so ∠3 = ∠2                                 (Corresponding angles axiom)

Therefore, ∠1 = ∠3                                        (Commutative property)

But ∠1 and ∠3 are corresponding angles and they are equal.

So by the converse of corresponding angles axiom, it can be deduced that a || c.

Parallel Lines: Theorem

• The lines which are parallel to the same line are parallel to each other as well.
• This property holds good for more than 2 lines also.

Example

In the following figure, m, n, and l are parallel lines. And AB is parallel to CD. Find the value of angle x using the given angles.

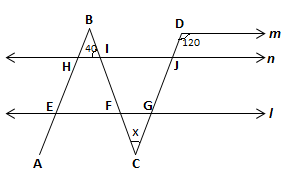
Solution:

Since m || l, ∠CGI = 120°                                (Corresponding angles)

∠FGC = 180° – 120° = 60°                             (Linear pair with ∠CGI)

∠BIH = ∠BFE = 40°                                         (Corresponding angles)

∠BFE = ∠GFC = 40°                                        (Vertically opposite angles)

Therefore, x + 40° + 60° = 180°                    (Sum of angles of a triangle is 180°)

Or x = 180° – 100° = 80°

Conditions for Lines to be parallel

If two straight lines are cut by a transversal,

• the pair of alternate angles is equal, then two straight lines are parallel to each other.
• the pair of interior angles are on the same side of traversals is supplementary, then the two straight lines are parallel.
• the pair of corresponding angles are equal, then the two straight lines are parallel to each other.

To know more about what are parallel lines and their related terms download BYJU’S – The Learning App.