Rotation
Rotation meaning in Maths can be given based on geometry. Thus, it is defined as the motion of an object around a centre or an axis. Any rotation is considered as a motion of a specific space that freezes at least one point. We know the earth rotates on its axis in real life, also an example of rotation. In Geometry, there are four basic types of transformations. They are
- Rotation
- Reflection
- Translation
- Resizing
In this article, you will learn about one of the transformation types called “Rotation” in detail along with its definition, formula, rules, rotational symmetry and examples.
| Table of Contents: |
Rotation Definition
Rotation means the circular movement of an object around a centre. It is possible to rotate different shapes by an angle around the centre point. Mathematically, a rotation means a map. All the rotations around a fixed point that make a group under a structure are called the rotation group of a unique space. When coming to the three-dimensional shapes, we can turn or rotate the objects about an infinite number of imaginary lines known as rotational axes. Now one might have the question of what the rotation of axes is? Here is the answer. The rotations around X, Y and Z axes are known as the principal rotations. The rotations around any axis can be performed by taking the rotation around the X-axis, followed by the Y-axis and then finally the z-axis.
| Read more: |
Rotation Formula
Rotation can be done in both directions like clockwise as well as counterclockwise. The most common rotation angles are 90°, 180° and 270°. However, a clockwise rotation implies a negative magnitude, so a counterclockwise turn has a positive magnitude. There are specific rules for rotation in the coordinate plane. They are:
| Type of Rotation | A point on the Image | A point on the Image after Rotation |
| Rotation of 90°
(Clockwise) |
(x, y) | (y, -x) |
| Rotation of 90°
(Counter Clockwise) |
(x, y) | (-y, x) |
| Rotation of 180°
(Both Clockwise and Counterclockwise) |
(x, y) | (-x, -y) |
| Rotation of 270°
(Clockwise) |
(x, y) | (-y, x) |
| Rotation of 270°
(Counter Clockwise) |
(x, y) | (y, -x) |
Rotation Matrix
A rotation matrix is a matrix used to perform a rotation in a Euclidean space. In a two-dimensional cartesian coordinate plane system, the matrix R rotates the points in the XY-plane counterclockwise through an angle θ about the origin. The matrix R can be represented as:
\(R=\begin{bmatrix} cos\ \theta & -sin\ \theta\\ sin\ \theta & cos\ \theta \end{bmatrix}\)
If we want to perform the rotation operation using the rotation matrix R, the position of each point in the plane is represented by a column vector “v”, which contains the coordinate point. With the help of matrix multiplication Rv, the rotated vector can be obtained.
Rotational Symmetry
In geometry, many shapes have rotational symmetry like circles, squares, and rectangles, etc. All the regular polygons have rotational symmetry. If an object is rotated around its centre, the thing appears precisely like before the rotation. Then the object is said to have rotational symmetry. We can identify the rotation symmetry in many ways. One of the easiest ways to find the order of symmetry is to count the number of times the figure coincides with itself when it rotates through 360°.
Rotation Images
The below figure shows the rotational symmetry of a geometric figure.
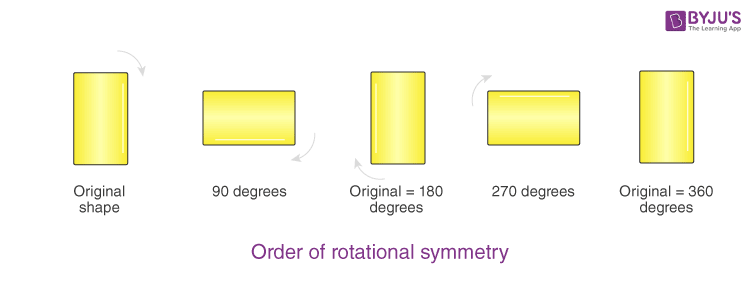
The above example shows the rotation of a rectangle 90° each time. The rectangle has the rotational symmetry of order 2 because when it is rotated twice, we get the original shape at 180° and again, when it is rotated twice, the original form is obtained at 360°. So, the order of rotational symmetry of the rectangle is 2.
Learn more about rotational symmetry along with examples here.
Rotation Examples
In this section, you can observe the real life examples of rotation that may denote the axis rotation.
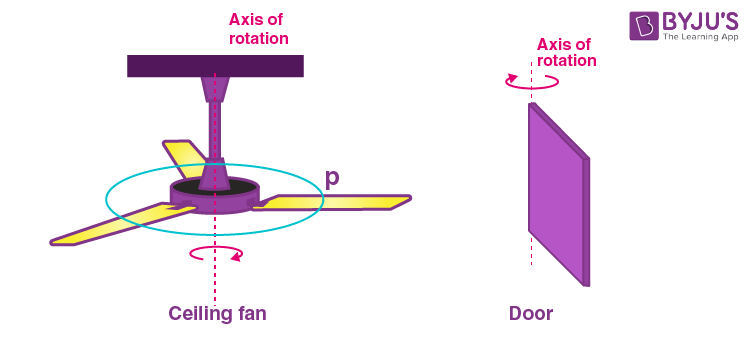
In the above figure, the motion of a ceiling fan and the movement of a door shows the axis of rotation.
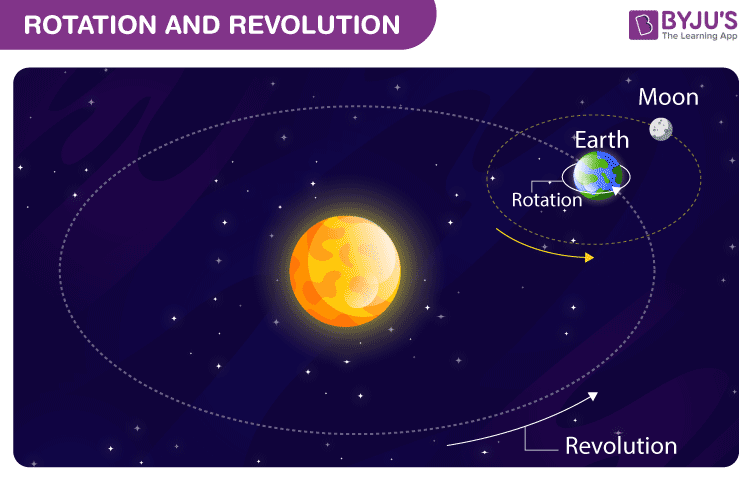
Rotation and Revolution
When it comes to the revolution, everyone is often confused with rotation. Most people think that rotation and revolution are the same. However, there is a difference between these two terms. This can be well explained with the example of rotation of Earth as shown in the figure given below:
Watch the Below Video To Understand The Rotation Concept Using Patterns

Stay tuned with BYJU’S – The Learning App for interesting maths-related articles and also watch personalised videos to learn with ease.
Frequently Asked Questions on Rotation
What is rotation in Maths?
The rotation is a type of transformation in Maths is the circular motion of an object around a centre or an axis or a fixed point.
What are the examples of rotation?
In real-life, we know the earth rotates on its own axis, which is an example of rotation.
A group of people holding their hands and forming a circle and walking in a clockwise or anticlockwise direction.
A globe of map rotating on its axis.
What are the types of rotation?
The rotation could be clockwise or counterclockwise. If there is an object which is to be rotated, it can be done by following different ways:
90 degrees clockwise
90 degrees anticlockwise
180 degrees clockwise
180 degrees anticlockwise
What is a point of rotation and angle of rotation?
The point about which the object is rotated is the point of rotation.
The amount of rotation measured in degrees is called the angle of rotation.