The following equalities in trigonometry will be used in the upcoming discussion to establish a relation between the sum and difference of angles

cos (-x) = cos x

sin (-x) = -sin x

We will now focus on the trigonometric functions which involve the sum and difference of two angles.

Trigonometric functions of sum and difference of angles

Consider the following figure:

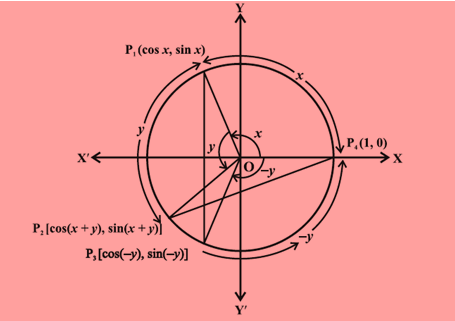
A circle is drawn with center as origin and radius 1 unit. A point P₁ is chosen at an angle of x units from x-axis. The co-ordinates are mentioned in the figure. Another point P₂ is chosen, at an angle of y units from the line segment OP₁. P₃ is a point on the circle which is at an angle of y units from x-axis, measured clockwise.

Now, in the given figure, Δ OP₁P₃ is congruent to Δ OP₂P₄, by SAS congruency criteria.

Hence, P₁P₃ = P₂P₄ (CPCT)

⇒(P₁P₃ )²= (P₂P₄)²

Since we know the coordinates of all the four points, hence using distance formula, we can write:

[cos x – cos (-y)]² + [sin x – sin (-y)]² = [1- cos (x+y)]² + sin² (x+y)

On solving the above equation, we have the following identity:

cos(x + y) = cos x cos y – sin x sin y ……… (1)

Replacing y by  -y in identity (1), we get,

cos(x – y) = cos x cos y + sin x sin y …….… (2)

Also,

cos (π/2 – x) = sin x ……………… (3)

That can be obtained by replacing x by π/2 and y by x in identity (2). Also,

sin (π/2 – x) = cos x………….…… (4)

As, sin (π/2 – x) = cos [π/2 – (π/2 – x)] (using identity 3). So,

sin (π/2 – x) = cos x

Now we have the idea about the expansion of sum and difference of angles of cos. Now let us try to use it for finding the values of sum and difference of angles of sin.

sin (x + y) can be written as cos [π/2 – (x + y)] which is equal to cos [(π/2 – x) – y]

Now, using identity (2)  we can write,

cos [(π/2 – x) – y] = cos (π/2 – x) cos y + sin (π/2 – x) sin y

= sin x cos y + cos x sin y

Hence,

sin (x + y) = sin x cos y + cos x sin y …………………………. (5)

Replace y by –y in the above formula, we get

sin (x – y) = sin x cos y – cos x sin y .…………………………….. (6)

Now if we substitute suitable values in identities (1), (2), (5) and (6), we have the following:

cos (π/2 + x) = -sin x

sin (π/2 + x) = cos x

cos (π± x) = – cos x

sin (π – x) = sin x

sin (π + x) = – sin x

sin (2π – x) = -sin x

cos (2π – x) = cos x

After having a brief idea about the expansion of sum and difference of angles of sin and cos, the expansion for tan and cot is given by

tan (x + y) = (tan x + tan y)/ (1-tan x tan y)

tan (x – y) = (tan x – tan y)/ (1+tan x tan y)

Similarly;

cot (x + y) = (cot x cot y – 1)/(cot y + cot x)

cot (x – y) = (cot x cot y + 1)/(cot y – cot x)

To learn more about trigonometric functions and sum and difference of angles, please download BYJU’S- The Learning App.