Supplementary And Complementary Angles
Supplementary angles and complementary angles are defined with respect to the addition of two angles. If the sum of two angles is 180 degrees then they are said to be supplementary angles, which forms a linear angle together. Whereas if the sum of two angles is 90 degrees, then they are said to be complementary angles, and they form a right angle together.
When two line segments or lines meet at a common point (called vertex), at the point of intersection an angle is formed. When a ray is rotated about its endpoint, then the measure of its rotation in an anti-clockwise direction is the angle formed between its initial and final position.
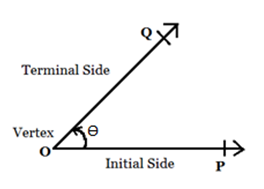
In fig. 1 if the ray \(\small \overrightarrow{OP}\) is rotated in the direction of the ray \(\small \overrightarrow{OQ}\), then the measure of its rotation represents the angle formed by it. In this case, the measure of rotation that is the angle formed between the initial side and the terminal side is represented by Ɵ.
Complementary Angles
When the sum of two angles is 90°, then the angles are known as complementary angles. In other words, if two angles add up to form a right angle, then these angles are referred to as complementary angles. Here we say that the two angles complement each other.
Suppose if one angle is x then the other angle will be 90o – x. Hence, we use these complementary angles for trigonometry ratios, where on ratio complement another ratio by 90 degrees such as;
- sin (90°- A) = cos A and cos (90°- A) = sin A
- tan (90°- A) = cot A and cot (90°- A) = tan A
- sec (90°- A) = cosec A and cosec (90°- A) = sec A
Hence, you can see here the trigonometric ratio of the angles gets changed if they complement each other.
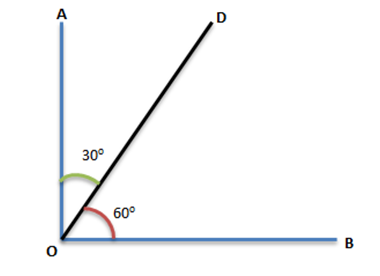
Complementary Angles
In the above figure, the measure of angle BOD is 60o and angle AOD measures 30o. On adding both of these angles we get a right angle, therefore ∠BOD and ∠AOD are complementary angles.
The following angles in Fig. 3 given below are complementary to each other as the measure of the sum of both the angles is 90o. ∠POQ and ∠ABC are complementary and are called complements of each other.
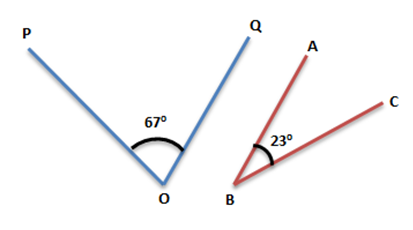
Complementary Angles Example
For example: To find the complement of 2x + 52°, subtract the given angle from 90 degrees.
90o – (2x + 52o) = 90o – 2x – 52o = -2x + 38o
The complement of 2x + 52o is 38o – 2x.
Facts of complementary angles:
|
Supplementary Angles
When the sum of two angles is 180°, then the angles are known as supplementary angles. In other words, if two angles add up, to form a straight angle, then those angles are referred to as supplementary angles.
The two angles form a linear angle, such that, if one angle is x, then the other the angle is 180 – x. The linearity here proves that the properties of the angles remain the same. Take the examples of trigonometric ratios such as;
- Sin (180 – A) = Sin A
- Cos (180 – A) = – Cos A (quadrant is changed)
- Tan (180 – A) = – Tan A
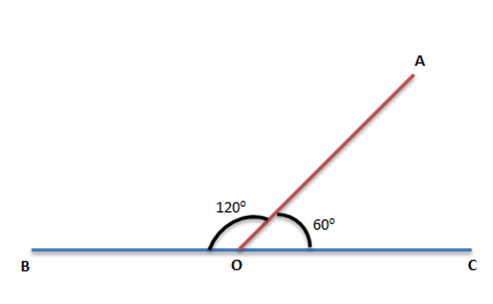
Supplementary Angles
In Fig. 4 given above, the measure of ∠AOC is 60o and ∠AOB measures 120o. On adding both of these angles we get a straight angle. Therefore, ∠AOC and ∠AOB are supplementary angles, and both of these angles are known as a supplement of each other.
Also, learn:
Difference between Complementary and Supplementary Angles
| Complementary Angles | Supplementary Angles |
| Sum is equal to 90 degrees | Sum is equal to 180 degrees |
| Two angles complement each other | Two angles supplement each other |
| It is not defined for linear pair of angles | It is defined for linear pair of angles |
| Meant only for right angles | Meant only for straight angles |
How to remember easily the difference between Complementary angle and supplementary angles?
- “C“ letter of Complementary stands for “Corner” (A right angle, 90o)
- “S“ letter of Supplementary stands for “Straight” ( a straight line, 180o)
Solved Examples
The example problems on supplementary and complementary angles are given below:
Example 1:
Find the complement of 40 degrees.
Solution:
As the given angle is 40 degrees, then,
Complement is 50 degrees.
We know that Sum of Complementary angles = 90 degrees
So, 40° + 50° = 90°
Example 2:
Find the Supplement of the angle 1/3 of 210°.
Solution:
Step 1: Convert 1/3 of 210°
That is, 1/3 x 210° = 70°
Step 2: Supplement of 70° = 180° – 70° = 110°
Therefore, Supplement of the angle 1/3 of 210° is 110°
Example 3:
The measures of two angles are (x + 25)° and (3x + 15)°. Find the value of x if angles are supplementary angles.
Solution:
We know that, Sum of Supplementary angles = 180 degrees
So,
(x + 25)° + (3x + 15)° = 180°
4x + 40° = 180°
4x = 140°
x = 35°
The value of x is 35 degrees.
Example 4:
The difference between two complementary angles is 52°. Find both the angles.
Solution:
Let, First angle = m degrees, then,
Second angle = (90 – m)degrees {as per the definition of complementary angles}
Difference between angles = 52°
Now,
(90° – m) – m = 52°
90° – 2m = 52°
– 2m = 52° – 90°
-2m = -38°
m = 38°/2°
m = 19°
Again, Second angle = 90° – 19° = 71°
Therefore, the required angles are 19°, 71°.
Practice Questions
- Check if 65° and 35° are complementary angles.
- Is 80° and 100° supplementary?
- Find the complement of 54°.
- Find the supplement of 99°.
- If one angle measures 50° and is supplementary to another angle. Then find the value of another angle. Also, state what type of angle it is?
Frequently Asked Questions – FAQs
What are complementary angles? Give example.
What are supplementary angles? Give examples.
How to find complementary angles?
For example, if one of the two angles is 45 degrees, then;
x + 45 = 90
x = 90 – 45 = 45°
What is the complementary angle of 40 degrees?
90 – 40 = 50 degrees
How to find supplementary angles?
For example, if one angle is 60 degrees, then another angle is 180 – 60 = 120 degrees.