The converse of Pythagoras theorem states that “If the square of a side is equal to the sum of the square of the other two sides, then triangle must be right angle triangle”. Whereas Pythagorean theorem states that the sum of the square of two sides (legs) is equal to the square of the hypotenuse of a right-angle triangle. But, in the reverse of the Pythagorean theorem, it is said that if this relation satisfies, then triangle must be right angle triangle. So, if the sides of a triangle have length, a, b and c and satisfy given condition a² + b² = c², then the triangle is a right-angle triangle.

Let us see the proof of this theorem along with examples.

Converse of Pythagoras Theorem Proof

Statement: If the length of a triangle is a, b and c and c² = a² + b², then the triangle is a right-angle triangle.

Proof: Construct another triangle, △EGF, such as AC = EG = b and BC = FG = a.

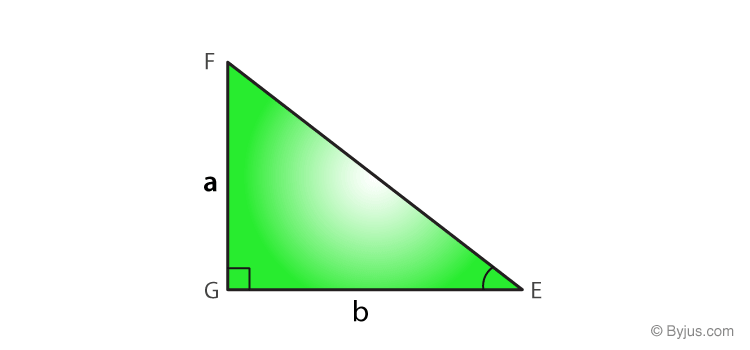
In △EGF, by Pythagoras Theorem:

EF² = EG² + FG² = b² + a² …………(1)

In △ABC, by Pythagoras Theorem:

AB² = AC² + BC² = b² + a² …………(2)

From equation (1) and (2), we have;

EF² = AB²

EF = AB

⇒ △ ACB ≅ △EGF (By SSS postulate)

⇒ ∠G is right angle

Thus, △EGF is a right triangle.

Hence, we can say that the converse of Pythagorean theorem also holds.

Hence Proved.

Formula

As per the converse of the Pythagorean theorem, the formula for a right-angled triangle is given by:

Where a, b and c are the sides of a triangle.

Applications

Basically, the converse of the Pythagoras theorem is used to find whether the measurements of a given triangle belong to the right triangle or not. If we come to know that the given sides belong to a right-angled triangle, it helps in the construction of such a triangle. Using the concept of the converse of Pythagoras theorem, one can determine if the given three sides form a Pythagorean triplet.

Converse of Pythagoras Theorem Examples

Question 1: The sides of a triangle are 5, 12 and 13. Check whether the given triangle is a right triangle or not?

Solution: Given,

a = 5

b = 12

c = 13

By using the converse of Pythagorean Theorem,

a²+b² = c²

Or

c² = a²+b²

Substitute the given values in the above equation,

13² = 5²+12²

169 = 25 + 144

169 = 169

So, the given lengths are does not satisfy the above condition.

Therefore, the given triangle is a right triangle.

Question 2: The sides of a triangle are 7, 11 and 13. Check whether the given triangle is a right triangle or not?

Solution: Given;

a = 7

b = 11

c = 13

By using the converse of Pythagorean Theorem,

c² = a²+b²

Substitute the given values in the the above equation,

13² = 7² + 11²

169 = 49 + 121

169 = 170

So, it is not satisfied with the above condition.

Therefore, the given triangle is not a right triangle.

Question 3: The sides of a triangle are 4,6 and 8. Say whether the given triangle is a right triangle or not.

Solution: Given: a = 4, b = 6, c = 8

By the converse of Pythagoras theorem

a²+b² = c²

8² = 4² + 6²

64 = 16 + 36

64 = 52

The sides of the given triangle do not satisfy the condition a²+b² = c².

Therefore, the given triangle is not a right triangle.