Convert Decimal to Fraction
To convert a decimal into a fraction, we need to first write the given decimal in the form of a fraction, by adding a denominator 1. Then we need to multiply both numerator and denominator with the multiples of 10, to remove decimal (.) from the given number. For example, 1.9 is a decimal number, then the equivalent fraction will be 19/10. We cannot simply 19/10 further.
Decimal: In terms of a computer, decimal numbers are the numbers that have a base 10. But in Mathematics, a decimal number is a number that has a dot(.) or decimal point between the digits. Basically, decimals are nothing but fractions with denominators as 10 or multiples of 10. For example, 3.2, 10.9, 55.1, 1.28, 9.234, etc., are decimals.
Table of Contents:
- How to Convert Decimal to Fraction
- Examples
- Repeating Decimal to Fraction
- Conversion table
- Problems
- FAQs
Fractions: Fraction is a part of a whole number. It is denoted as a ratio of two numbers a/b, where a and b are integers, also b≠0. The two numbers are called the numerator and denominator. For example, 1/2 is a part of 1, 3/5 is a part of 3, etc. We can perform all the arithmetic operations on fractions. There are three types of fractions, Proper, Improper and Mixed.
How to Convert Decimal into Fractions?
Now let us learn the steps to convert the decimal into fractions.
- First write the given decimal in the form of a ratio (p/q), where the denominator is equal to 1.
- Now multiply the numerator and denominator by multiples of 10, for every decimal point, such that the decimal in the numerator becomes a whole number. (If there are two numbers after the decimal point, then multiply by 100/100)
- Simply the resulting fraction
Also, read:
The below figure visualizes how to convert decimal to fraction with a simple example.
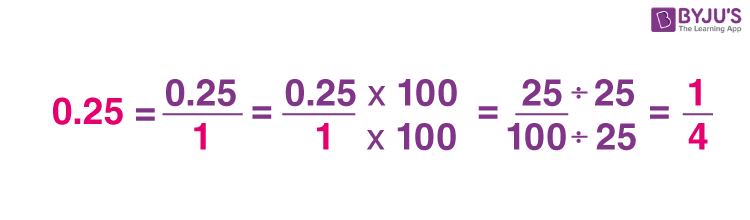
These steps make decimal to fraction conversion simple and easy. Using these steps, we can get accurate results.
Solved Examples
Solve problems based on conversion of decimal to fraction and fraction to decimal are given here. These examples of decimal to fraction conversions will help you in better understanding of the concept.
Question 1: Find the fraction form of the decimal 0.7
Solution: Given, decimal number 0.7, we need to find the fraction for 0.7.
We can also find a number of equivalent fractions by finding its multiples.
0.7 = 7/10
Now multiply, 7/10 by 2, both in numerator and denominator, then we get;
(7×2)/(10×2) = 14/20
To find more equivalent fractions, let us multiply 7/10 by 5 and 10 both in numerator and denominator.
7×5/10×5 = 35/50
7×10/10×10 = 70/100
Therefore, the fractions of 0.7 decimal are 7/10, 35/50, 70/100.
Question 2: Convert 7.15 into a fraction.
Solution: Given, 7.15 is a decimal number.
Multiply and divide 7.15 by 100.
7.15 × 100/100 = 715/100
If we simplify it more, we get;
143/20
We can also find the equivalent fractions by multiplying the numerator and denominator by 2. Such as;
143×2/20×2 = 286/40
So, 7.15 equivalent fractions are 715/100, 143/20 and 286/40.
Question 3: Convert 3.35 into a fraction.
Solution: Following the above steps:
3.35/1
Since there are two numbers after the decimal point, therefore, multiply 3.35/1 by 100 in numerator and denominator.
(3.35/1)x(100/100) = 335/100 = 67/20
Question 4: Convert 1.625 into a mixed fraction.
Solution: We can write 1.625 as 1.625/1
Multiply by 1000 to remove decimal up to three places
1.625/1 x (1000/1000) = 1625/1000
Simplifying 1625/1000 we get;
⇒ 13/8
Now converting into a mixed fraction.
13/8 = 1 5/8
Hence, 1 5/8 is the mixed fraction equivalent to 1.625.
Repeating Decimal to Fraction
To convert a usual decimal number to a fraction is an easy method. But to convert a repeating or recurring number to a fraction is a lengthy task. For example, 0.666…, 4.17777…, 0.56111.., are recurring numbers. Let us learn to convert recurring decimal to fraction with the help of an example.
Example: Convert 0.6666… Into fraction.
Solution: Let x = 0.6666
Now multiply x by 10 on both sides.
10 x = 6.666…
Subtracting x from 10x, we get;
10x-x = 6.666…-0.6666
9x = 6.000
x = 6/9 = ⅔
Decimal to Fraction Table
Let us see here some of the decimals written in the form of the fraction which is commonly used in mathematical calculation.
| Decimal | Fraction | Decimal | Fraction |
| 0.5 | 1/2 | 1.5 | 6/4 |
| 0.25 | 1/4 | 0.857142… | 6/7 |
| 0.6666… | 2/3 | 0.875 | 7/8 |
| 0.4 | 2/5 | 1.4 | 7/5 |
| 0.285714… | 2/7 | 3.333… | 10/3 |
| 0.2222 | 2/9 | 1.42857… | 10/7 |
| 0.75 | 3/4 | 1.875 | 15/8 |
| 0.428571… | 3/7 | 0.9375 | 15/16 |
| 2.5 | 5/2 | 0.95454… | 21/22 |
| 0.83333 | 5/6 | 0.78125 | 25/32 |
Worksheet
Convert the given decimals into fractions and simplify them.
- 9.25 (Answer: 37/4)
- 0.005 (Answer: 1/200)
- 10.010 (Answer: 1001/100)
- 99.95 (Answer: 1999/20 or 99 19/20)
- 0.42 (Answer: 21/50)
Frequently Asked Questions – FAQs
How do turn a decimal number into a fraction?
How to write decimal into mixed fraction form?
Now multiply numerator and denominator by 10.
(2.3/1) x (10/10) = 23/10
23 divided by 10 is 2 and remainder is 3
Therefore, 23/10 can be written as 2 3/10 in mixed fraction form.
What is 0.375 as a fraction?
= 375/1000
= ⅜
What is 1.75 as a fraction?
What is 0.625 as a fraction?
Multiply and divide by 1000 to get;
625/1000
Simplify to get
⅝