Distance between two points formula uses the coordinates of two points in space. In coordinate geometry, the distance between two points can be calculated using distance formula, present in a two-dimensional or three-dimensional space. The distance formula for two points is also an application of the Pythagoras theorem. Let us learn more in this article with examples.

What is Distance Between Two Points Formula?

Distance between two points is the length of the line segment that connects the two points in a plane. The formula to find the distance between the two points is usually given by d=√((x₂ – x₁)² + (y₂ – y₁)²).  This formula is used to find the distance between any two points on a coordinate plane or x-y plane.

Distance Formula for Two Points

As discussed, the distance formula is used to find the distance between any two points, when we already know the coordinates. The points could be present alone on the x-axis or y-axis or in both axes.

Let us consider, there are two points say A and B in an XY plane. The coordinates of point A are (x₁,y₁) and of B are (x₂,y₂). Then the formula to find the distance between two points PQ is given by:

\(AB = \sqrt{[x_{2}-x_{1}]^{2}+[y_{2}-y_{1}]^{2}}\)

Note: If the coordinates of two points P and Q are such that, (x₁, 0) and (x₂, 0), the distance between PQ will be given by:

PQ = |x₂ – x₁|

Distance Between Two Points on a Coordinate Plane

In case of a two-dimensional plane, the two points lie along x-axis and y-axis. The distance of a point from the y-axis is known as its x-coordinate or abscissa. The distance of a point from the x-axis is known as its y-coordinate, or ordinate. The coordinates of a point on the x-axis and y-axis are of the form (x, 0) and (0, y), respectively.

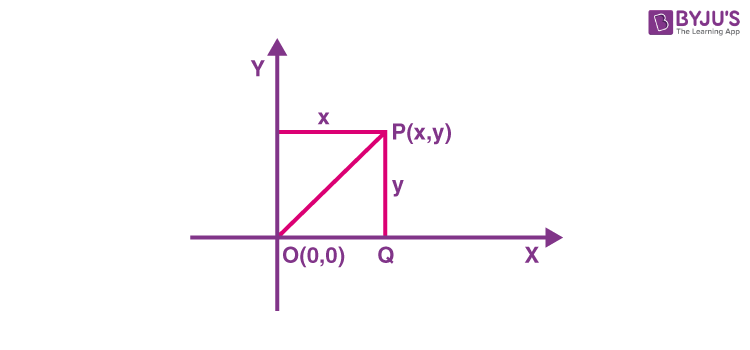
In the above graph, the distance between point origin O(0,0) and P(x,y) is given by:

OP = √((x₂ – 0)² + (y₂ – 0)²)

OP = √((x₂)² + (y₂)²)

or simply,

OP = √(x² + y²)

where x and y are coordinates of point other than origin.

Distance Between Two Points Formula in 3D Space

If we have to find the distance between the points in a three-dimensional space, then we consider here an extra coordinate which is present in the z-axis.

Let us consider two points A(x₁,y₁,z₁) and B(x₂,y₂,z₂) in 3d space. Then, the distance formula for these two points is given by;

\(AB = \sqrt{[x_{2}-x_{1}]^{2}+[y_{2}-y_{1}]^{2}+[z_{2}-z_{1}]^{2}}\)

Distance of any point P(x,y,z) in space from origin O(0,0,0), is given by,

\(AB = \sqrt{x^{2}+y^{2}+z^{2}}\)

Related Articles

• Distance Between Two Points
• Distance between Two Lines
• Midpoint theorem
• Distance Between Two Points in Three Dimensions

Solved Examples

Q.1: What is the distance between two points A and B whose coordinates are (3, 2) and (9, 7), respectively?

Solution: Given, A (3,2) and B(9,7) are the two points in a plane.

We have to find the distance between A and B.

Using distance between formula for two points, we know;

distance, d=√((x₂ – x₁)² + (y₂ – y1)²)

Here, x₁ = 3, x₂ = 9, y₁ = 2 and y₂ = 7.

Thus, putting all the values of x and y in the formula, we get;

d=√((9-3)² + (7-2)²)

d = √(6² + 5²)

d = √(36 + 25)

d = √61 unit.

Q.2: Find the distance of a point P(4, 3) from the origin.

Solution: Given, P(4, 3) is a point at a distance from the origin.

The coordinates of a point at the origin will be (0,0).

Using the distance between formula for two points, we know;

distance, d=√((x₂ – x₁)² + (y₂ – y1)²)

Here, x₁ = 4, x₂ = 0, y₁ = 3 and y₂ = 0.

Thus, putting all the values of x and y in the formula, we get;

d = √((0-4)² + (0-3)²)

d = √(4² + 3²)

d = √(16 + 9)

d = √25

d = 5 unit