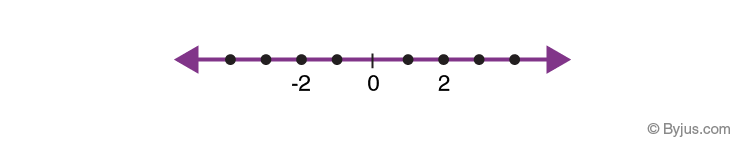
Absolute Values
The absolute value of a number refers to the distance of a number from the origin of a number line. It is represented as |a|, which defines the magnitude of any integer ‘a’. The absolute value of any integer, whether positive or negative, will be the real numbers, regardless of which sign it has. It is represented by two vertical lines |a|, which is known as the modulus of a.
For example: 5 is the absolute value for both 5 and -5.
|-5| = +5 and |+ 5| = +5
In this article, we will learn what is the absolute value of a number, symbol, examples, absolute value in number line, absolute value of real numbers, absolute value of complex numbers in detail.
| Table of Contents: |
What is the Absolute Value of a Number?
The absolute value of a number or integer is the actual distance of the integer from zero, in a number line. Therefore, the absolute value is always a positive value and not a negative number.
We can define the absolute values like the following:
{ a if a ≥ 0 }
|a| = { -a if a < 0 }
Note: There is no absolute value for 0 because the absolute value changes the sign of the numbers into positive and zero has no sign.
If the number is positive then it will result in a positive number only. And if the number is negative, then the modulus of this number will also be a positive number. It is denoted as |n|, where n is an integer.
Absolute Value Symbol
The symbol of absolute value is represented by the modulus symbol, ‘| |’, with the numbers between it. For example, the absolute value of 9 is denoted as |9|.
The distance of any number from the origin on the number line is the absolute value of that number. It also shows the polarity of the number whether it is positive or negative. It can be negative ever a s it shows the distance and the distance can’t be negative. So, it is always positive.
| ‘| |’ – Absolute value symbols, ‘| | pipes’ are used to represent the absolute values.
For example: ‘|a|’, where “a” is the number whose absolute value has to be determined. |
Absolute value of a Number Examples
Let us see some examples of the absolute value of a number.
- |-1| = 1
- |-14| = 14
- |1| = 1
- |0| = 0
- |7| = 7
- |7-2| = |5| = 5
- |2+3| = |5| = 5
- |-3×5| = |-15| = 15
Related Articles:
Absolute Value Function
The absolute value function is given by f(x) = |x| such that:
- |x| = +x for x > 0
- |x| = -x for x < 0
Absolute Value Properties
If x and y are real numbers and then the absolute values are satisfying the following properties:
| Property | Expression |
| Non-negativity | | x | ≥ 0 |
| Positive-definiteness | | x | = 0 ↔ a = 0 |
| Multiplicativeness | | x × y| = |x| × |y| |
| Subadditivity | | x + y| ≤ | x | + | y | |
| Symmetry | |-x| = |x| |
| Identity of indiscernible (equivalent to positive definiteness) | | x – y | = 0 ↔ a = b |
| Triangle inequality (equivalent to subadditivity) | | x – y | ≤ | x – z | + | z – x | |
| Preservation of division (equivalent to multiplicativeness) | | x / y| = | x | / | y | |
| Equivalent to subadditivity | | x – y | ≥ | | x | – | y | | |
Absolute Value of a Real Number
If a real number x, the absolute value will satisfy the following conditions.
| x | = x, if x ≥ 0
| x | = – x, if x < 0
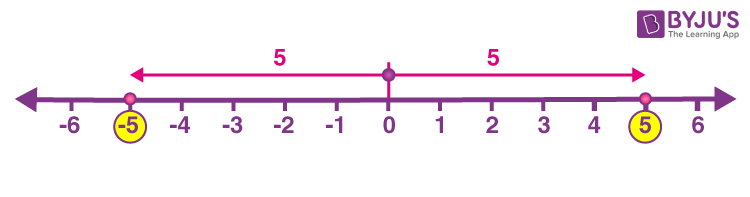
Let’s look at the absolute value of 2 in the number line given below. Here, |2| is the distance of 2 from 0(zero). So, both +2 and -2 is the distance of 2 from the origin. But it would be taken as 2 because distance is never measured in negative.
Absolute Value of Complex Number
Complex numbers consist of real numbers and imaginary numbers. Hence, unlike integers, it is difficult to find the absolute value for them. Suppose, x+iy is the given complex number.
z = x+iy
The absolute value of z will be;
|z|= √[Re(z)2+Im(z)2]
|z| = √(x2+y2)
Where x and y are the real numbers.
Absolute Value in Number Line
The graph of absolute values is called the absolute value graph. As we know the absolute value of any real number is positive, so the absolute value of any number or function graph will lie on the positive side only.
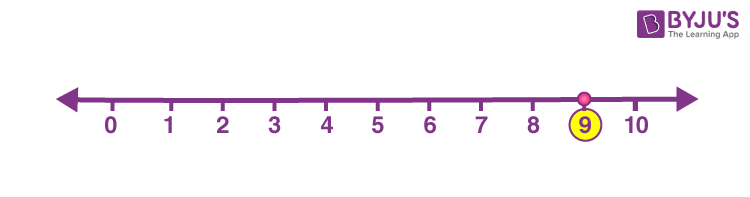
Example: Graph the absolute value of the number -9.
Solution: Absolute value of |-9| is +9.
So the graph for the absolute value of -9 will look like following
Problems and Solutions
Let’s understand this topic better with the help of examples.
Question 1:
Arrange the given numbers in ascending order.
-|-14|, |12|, |7|, |-91|, |-5|, |-8|, |-65|, |6|
Solution:
Initially, find the absolute values of the given numbers
-14, 12, 7, 91, 5, 8, 65, 6
Now, arrange the numbers in ascending order (smallest to the largest number)
-14, 5, 6, 7, 8, 12, 65, 91
Question 2:
Arrange the given numbers in ascending order.
-|-24|, |21|, 17|, |-109|, |-15|, |-19|, |-75|, |16|
Solution:
Find the absolute values of the given numbers
-24, 21, 17, 109, 15, 19, 75, 16
Now, arrange the numbers in ascending order (smallest to the largest number)
-24, 15, 16, 17,19, 21, 75, 109.
Example 3:
Find the absolute value of a number -12/5
Solution:
To find: |-12/5|
|-12/5| = 12/5
Hence, the absolute value of a number -12/5 is 12/5
Example 4:
Find the absolute value for the following numbers:
(a) |-1/2|
(b) |72|
(c) |3/4|
Solution:
The absolute value of the numbers are:
(a) |-1/2| = 1/2
(b) |72| = 72
Practice Questions
1. What is the absolute value of -13?
2. Find the absolute value of 100.
3. Arrange the following in ascending order.
|3|, |-9|, |1|, |-2|, |-5|
4. Plot the absolute value of -7 on the number line.
Stay tuned to BYJU’S – The Learning App and download the app to learn all Maths-related easily by exploring more videos.