Area Of Hexagon
The area of hexagon is the region occupied by it, within its six sides. A hexagon is a closed polygon made up of six line segments and six internal angles. The word hexagon is derived from the Greek words, ‘Hexa’ which mean six and ‘Gonia’ means corners. For a hexagon, the sum of internal angle always adds up to 720°. In this article, we will learn to find the area of the hexagon using these properties.
What is Area of the Hexagon?
Area of a hexagon is the area enclosed within its six sides. It is measured in square units such as m2, cm2, yard2,in2, etc. A hexagon is a two-dimensional closed shape that has six sides and six angles. All the sides are connected to each other through their end-points as shown in figure.

According to the length of sides, the hexagon can be of two types,
(i) Regular Hexagon: A regular hexagon is one whose all 6 sides are equal in length. Also, the internal angle is equal to \(120^{\circ}\). The regular hexagon consists of six symmetrical lines and rotational symmetry of order of 6.
(ii) Irregular Hexagon: An irregular hexagon is one whose all the sides are of unequal length and angles are of unequal measures.
In this article, we are going to learn the area of a regular hexagon, formula, its derivation and examples based on it.
Area of Hexagon Formula
The formula for area of hexagon is given by:
| Area of hexagon = (3√3 s2)/2 |
where ‘s’ is the length of side of regular hexagon.
Let us see how to derive this formula.
Derivation of Area of Hexagon
The area of the Hexagon has been derived as follows.
Step 1: In the first step, we consider a regular Hexagon with a side length of ‘s’.
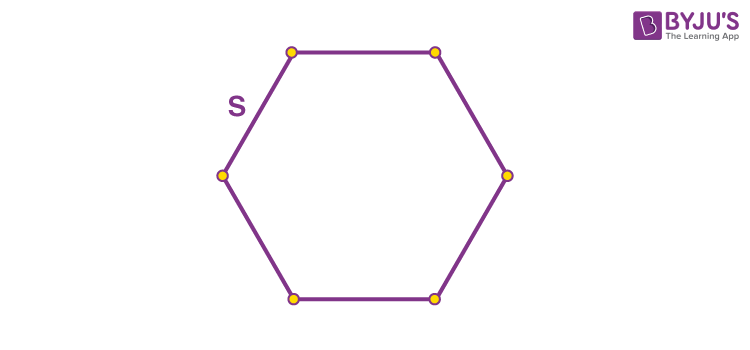
Step 2: In the second step, we divide the regular hexagon into six equal parts by connecting the opposite vertices with the other vertices. When you observe it, you can see that the hexagon is divided into six triangles.
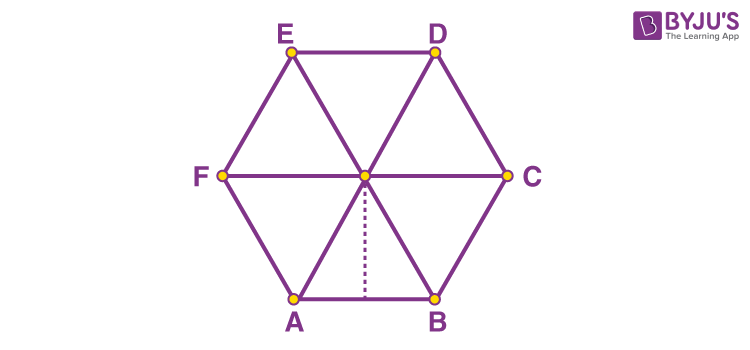
Step 3: We know that the area of a right-angled triangle is:
Area = 1/2 (Base) (Height)
Area = 1/2 (s.h)
Where “s” and “h” stand for the base and the height of the triangle, respectively.
Step 4: The Area of each of the triangle has been computed in the step (3). As there are six similar triangles, therefore the total area of the desired hexagon has been computed as:
Area of Hexagon = 6 x 1/2 (s.h) = 3.s.h
Where \(h^{2} = s^{2} – \left ( \frac{s}{2} \right )^{2}\) (By Pythagoras theorem)
\(h = \frac{\sqrt{3}}{2}s\)
Therefore, Area of Hexagon = \(A = \frac{3\sqrt{3}}{2}s^{2}\)
Thus, the formula for the area of the hexagon is obtained.
Similarly, for other polygons such as octagon, pentagon etc. we can also compute the area.
How to Find Area of Hexagon?
Using the formula derived above, we can find the area of the hexagon.
Area of hexagon = (3√3 s2)/2
- Step 1: Find the length of the side of regular hexagon
- Step 2: Evaluate the area using the formula of area of the hexagon (3√3 s2)/2, where ‘s’ is the side length of hexagon.
Area of Hexagon Using Apothem
Apothem is the straight line drawn from the center and is perpendicular to the side of the hexagon. Thus, using the apothem, the area of hexagon is given by:
A = 1/2 × Apothem × Perimeter of hexagon
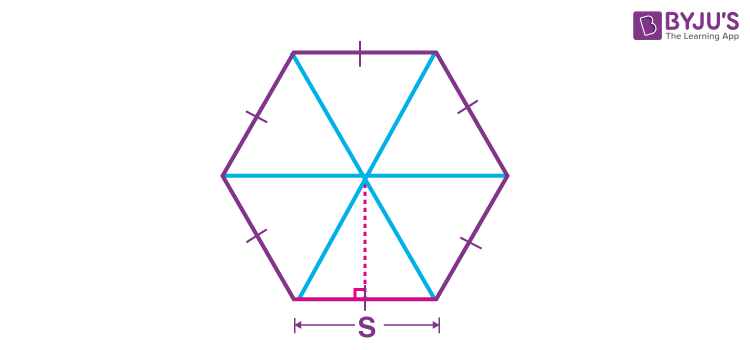
Since the perimeter of hexagon is equal to sum of all its sides. If the hexagon is regular and its sides is equal to s, then the perimeter is given by:
Perimeter of hexagon = 6s
Hence,
Area of hexagon = 1/2 × a × 6s = 3as
where ‘a’ is the apothem of the regular hexagon and ‘s’ is the length of the side of a regular hexagon.
Related Articles
Solved Examples on Area of Hexagon
Q.1: What is the area of a regular hexagon whose side length is equal to 5 cm?
Solution: By the formula, we know;
Area of hexagon = (3√3 s2)/2
A = (3√3 (5)2)/2
A = 65 sq.cm
Q.2: If the apothem of a regular hexagon is 4 cm and the side length is 3 cm, then find the area of hexagon.
Solution: Given, apothem of hexagon is a = 4 cm
Side length is s = 3 cm
By the formula, we know;
Area of hexagon = 3as
Area = 3 x 4 x 3 = 36 sq.cm.
Frequently Asked Questions on Area of Hexagon
What is the area of hexagon?
What is the formula for area of hexagon?
What is the formula of area of hexagon using apothem?
Area = 3 x Apothem x Side
What is the perimeter of hexagon?
To know more about the other characteristics and attributes of polygons such as hexagon, pentagon, octagon and other geometrical figures download BYJU’S-The Learning App.