Area of Rectangle
In geometry, area of rectangle is the region covered by the rectangle in a two-dimensional plane. A rectangle is a type of quadrilateral, a 2d shape that has four sides and four vertices. All the four angles of the rectangle are right angles or equal to 90 degrees. The opposite sides of the rectangle are equal and parallel to each other. To be noted, a parallelogram also has its opposite sides equal and parallel to each other but the angles are not equal to 90 degrees.
| Table of Contents: |
What is the Area of Rectangle?
Definition: Area of rectangle is the region occupied by a rectangle within its four sides or boundaries.
The area of a rectangle depends on its sides. Basically, the formula for area is equal to the product of length and breadth of the rectangle. Whereas when we speak about the perimeter of a rectangle, it is equal to the sum of all its four sides. Hence, we can say, the region enclosed by the perimeter of the rectangle is its area. But in the case of a square, since all the sides are equal, therefore, the area of the square will be equal to the square of side-length.
| Area of rectangle = Length x Breadth
A = lb |
Area of Rectangle Formula
The formula to find the area of rectangle depends on its length and width. The area of a rectangle is calculated in units by multiplying the width (or breadth) by the Length of a rectangle. Lateral and total surface areas can be calculated only for three-dimensional figures. We cannot calculate for the rectangle since it is a two-dimensional figure. Thus, the perimeter and the area of a rectangle is given by:
| The formula for the Area of a Rectangle | |
|---|---|
| Area of a Rectangle | A = l × b |
The area of any rectangle is calculated, once its length and width are known. By multiplying length and breadth, the rectangle’s area will obtain in a square-unit dimension. In the case of a square, the area will become side2. The main difference between square and rectangle is that the length and breadth are equal for square.
How to Calculate the Area of a Rectangle
Follow the steps below to find the area:
Step 1: Note the dimensions of length and width from the given data
Step 2: Multiply length and width values
Step 3: Write the answer in square units
Area of Rectangle Using Diagonal
We know that the diagonal of a rectangle is calculated using the formula:
(Diagonal)2 = (Length)2 + (Width)2
From this,
(Length)2 = (Diagonal)2 – (Width)2
Length = \(\sqrt{Diagonal^2 – Width^2}\)
Or
(Width)2 = (Diagonal)2 – (Length)2
Width = \(\sqrt{Diagonal^2 – Length^2}\)
Now, the area of rectangle = Length × Width
Area = Length × \(\sqrt{Diagonal^2 – Length^2}\)
Or
Area = \(\sqrt{Diagonal^2 – Width^2}\) × Width
Important Facts
Below are some special formulas related to the rectangle area.
- How to find the area with diagonal of rectangle and width
Formula: Area = \(Width\ \sqrt{(Diagonal^2 – Width^2)}\)
- Find a missing side length when the area is known
Formula: Length = Area/Width
Why Area of the rectangle is length x breadth?
The diagonals of the rectangle divide it into two equivalent right-angled triangles. Therefore, the area of the rectangle will be equal to the sum of the area of these two triangles.
Suppose, ABCD is a rectangle.
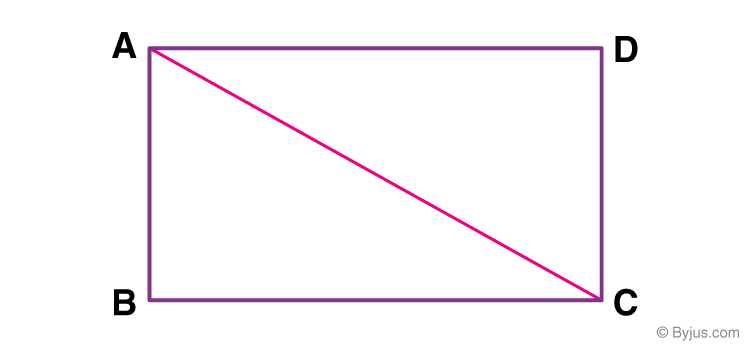
Now, let diagonal AC divide the rectangle into two right triangles, i.e. ∆ABC and ∆ADC.
We know that ∆ABC and ∆ADC are congruent triangles.
Area of ∆ABC = ½ x base x height = ½ x AB x BC = ½ x b x l
Area of ∆ADC = ½ x base x height = ½ x CD x AD = ½ x b x l
Area of rectangle ABCD = Area of ∆ABC + Area of ∆ADC
Area (ABCD) = 2(½ x b x l)
Area (ABCD) = l x b
Thus, the area of the rectangle = Length x Breadth
Related Articles
- Area Of A Triangle
- Area Of Square
- Area Of Quadrilateral
- Area Of Rhombus
- Area Of Trapezium
- Area Of Parallelogram
- Area of Circle
Area of rectangle Solved Examples
Example 1: Find the area of the rectangle whose length is 15 cm and the width is 4 cm.
Solution:
Given,
Length = 15 cm
Width = 4 cm
Area of a rectangle = Length × Width
15 × 4 = 60
So the area of rectangle = 60 cm2
Example 2: Find the area of a rectangular blackboard whose length and breadth are 120 cm and 100 cm, respectively.
Solution:
Length of the blackboard = 120 cm = 1.2 m
Breadth of the blackboard = 100 cm = 1 m
Area of the blackboard = area of a rectangle = length x breadth = 1.2 m x 1 m = 1.2 square-metres
Example 3: The length of a rectangular screen is 15 cm. Its area is 180 sq. cm. Find its width.
Solution:
Area of the screen = 180 sq. cm.
Length of the screen = 15 cm
Area of a rectangle = length x width
So, width = area/length
Thus, width of the screen = 180/15 = 12 cm
Example 4: The length and breadth of a rectangular wall are 75 m and 32 m, respectively. Find the cost of painting the wall if the rate of painting is Rs 3 per sq. m.
Solution:
Length of the wall = 75 m
The breadth of the wall = 32 m
Area of the wall = length x breadth = 75 m x 32 m = 2400 sq. m
For 1 sq. m of painting costs Rs 3
Thus, for 2400 sq. m, the cost of painting the wall will be = 3 x 2400 = Rs 7200
Example 5: A floor whose length and width is 50 m and 40 m respectively needs to be covered by rectangular tiles. The dimension of each tile is 1 m x 2 m. Find the total number of tiles that would be required to fully cover the floor.
Solution:
Length of the floor = 50 m
The breadth of the floor = 40 m
Area of the floor = length x breadth = 50 m x 40 m = 2000 sq. m
Length of one tile = 2 m
The breadth of one tile = 1 m
Area of one tile = length x breadth = 2 m x 1 m = 2 sq. m
No. of tiles required = area of floor/area of a tile = 2000/2 = 1000 tiles
Frequently Asked Questions on Area of Rectangle
What is the formula for area of rectangle?
Area = Length x Breadth
What is the perimeter of rectangle?
Perimeter (rectangle) = 2 (Length + Breadth)
What is the area of rectangle?
Why is the area of rectangle LB?
What is the unit of area?
Learn more about the rectangle, perimeter of a rectangle, quadrilaterals etc. by visiting our page BYJU’S.
