Areas Of Parallelograms And Triangles Class 9 Notes: Chapter 9
CBSE Class 9 Maths Areas Of Parallelograms And Triangles Notes:-Download PDF Here
Areas of parallelograms and triangles for class 9 notes are given here. Here, we are going to discuss some of the geometrical figures. A detailed explanation of areas of parallelograms and triangles are explained below with many theorems and proofs. Go through the below article and get the complete notes here to learn in an easy way.
Introduction
The area represents the amount of planar surface being covered by a closed geometric figure.
Areas of closed figures
Figures on the Common Base and Between the Same Parallels
Two shapes are stated to be on the common base and between the same parallels if:
a) They have a common side.
b) The sides parallel to the common base and vertices opposite the common side lie on the same straight line parallel to the base.
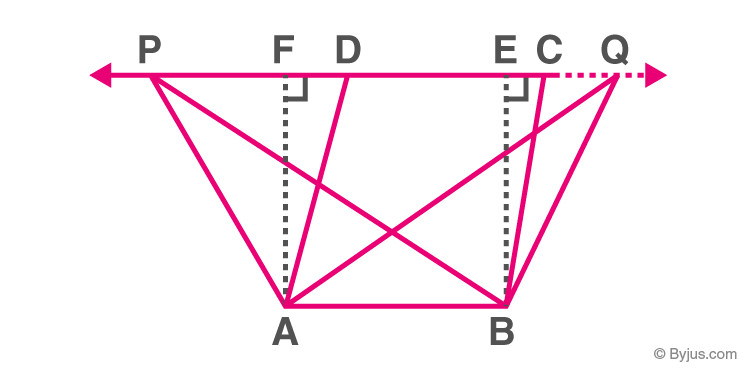
For example Parallelogram ABCD, Rectangle ABEF and Triangles ABP and ABQ
Area of a parallelogram

Parallelogram
Area of a parallelogram = b×h
Where ‘b′ is the base and ‘h′ is the corresponding altitude(Height).
To know more about Area of a Parallelogram, visit here.
Area of a triangle
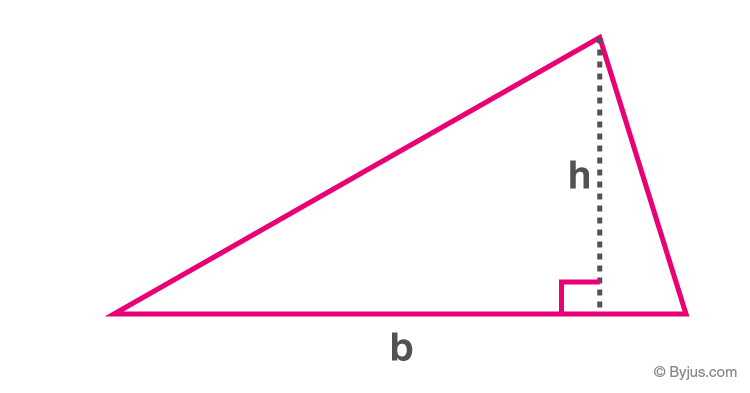
Area of triangle
Area of a triangle = (1/2)×b×h
Where “b” is the base and “h” is the corresponding altitude.
To know more about Area of a Triangle, visit here.
Theorems
Parallelograms on the Common Base and Between the Same Parallels
Two parallelograms are said to be on the common/same base and between the same parallels if
a) They have a common side.
b) The sides parallel to the common side lie on the same straight line.
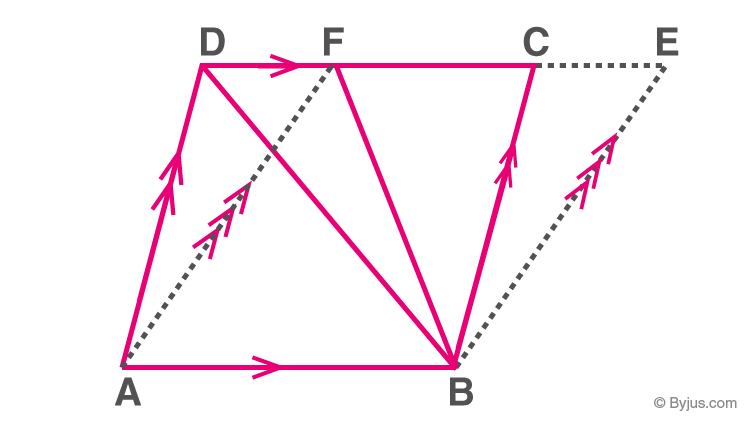
Parallelogram ABCD and ABEF
Theorem: Parallelograms that lie on the common base and between the same parallels are said to have equal in area.
Here, ar(parallelogram ABCD)=ar(parallelogram ABEF)
Triangles on the Common Base and Between the Same Parallels
Two triangles are said to be on the common base and between the same parallels if
a) They have a common side.
b) The vertices opposite the common side lie on a straight line parallel to the common side.

Triangles ABC and ABD
Theorem: Triangles that lie on the same or the common base and also between the same parallels are said to have an equal area.
Here, ar(ΔABC)=ar(ΔABD)
Two Triangles Having the Common Base & Equal Areas

If two triangles have equal bases and are equal in area, then their corresponding altitudes are equal.
A Parallelogram and a Triangle Between the Same parallels
A triangle and a parallelogram are said to be on the same base and between the same parallels if
a) They have a common side.
b) The vertices opposite the common side lie on a straight line parallel to the common side.
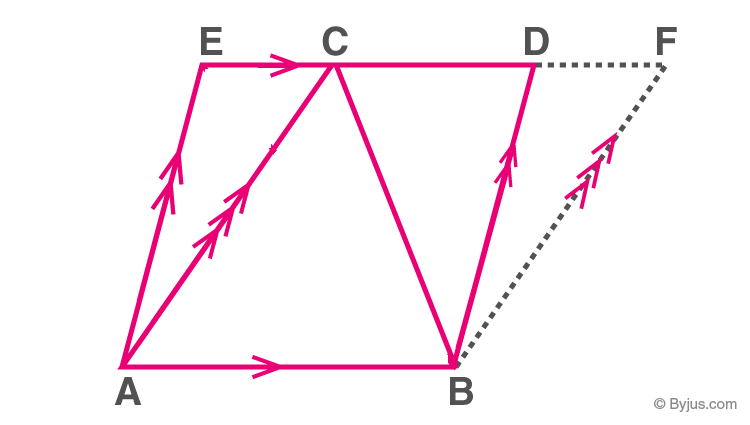
A triangle ABC and a parallelogram ABDE
Theorem: If a triangle and a parallelogram are on the common base and between the same parallels, then the area of the triangle is equal to half the area of the parallelogram.
Here, ar(ΔABC)=(1/2) ar(parallelogarm ABDE)