Convert Hexadecimal To Octal
In the number system, we come across four different types of the number system, i.e. hexadecimal, octal, decimal and binary. The conversion of these numbers from one form to another is possible. To convert hexadecimal to octal numbers, we need to convert hexadecimal to its equivalent decimal number first and then decimal to octal. Before this conversion, first, go through the basic definition of hexadecimal and octal numbers.
What Are Hexadecimal Numbers?
Hexadecimal numbers are the numbers which have base 16. It uses 16 different digits to represent the numbers. It is denoted as h16, where h is a hexadecimal number. It may be a combination of alphabets and numbers. Thus, it includes numbers from 0 to 9 and alphabets A to F.
Example: (AB2)16, (98D1)16, (AFD)16
What are Octal Numbers?
Octal numbers have base 8. These numbers use digits from 0 to 7, total 8 digits and hence, they are called octal number system. Octal numbers have base 8. It is denoted as o8 and o is an octal number. It does not use digits 8 and 9 to represent a number.
Example: (112)8, (275)8,(45)8
Hexadecimal to Octal Conversion
Conversion of hexadecimal to octal cannot be done directly. Firstly we need to convert hexadecimal into its equivalent decimal number then decimal to octal. Follow the steps below to understand the process.
- Consider the given hexadecimal number
- First count the number of digits in the number
- If n is the position of the digit from the right end then multiply each digit with 16n-1
- Add the terms after multiplication
- Resultant is the equivalent decimal form
- Divide the decimal number with 8
- Note down the remainder
- Repeat the previous two steps with the quotient, until the quotient is zero
- Write the remainders in reverse order
- The obtained number is the required result
Also, read:
Another Method to Convert Hex to Octal
There is another method to convert any hexadecimal to its equivalent octal. As we know, hexadecimal numbers include binary digits; therefore, we can club these binary numbers into a pair so that we can relate it with the octal numbers. Let us check the method with steps and example:
- For each given hexadecimal number digit, write the equivalent binary number. If any of the binary equivalents are less than 4 digits, add 0’s to the left side.
- Combine and make the groups of binary digits from right to left, each containing 3 digits. Add 0’s to the left if there are less than 3 digits in the last group.
- Find the octal equivalent of each binary group.
Let us see an example here:
Example: Convert 1BC16 into an octal number.
Solution: Given, 1BC16 is a hexadecimal number.
1 → 0001, B → 1011, C →1100
Now group them from right to left, each having 3 digits.
000, 110, 111, 100
000→0, 110 →6, 111→7, 100→4
Hence, 1BC16 = 6748
Hex to Octal Conversion Table
| Hexadecimal | Octal | Equivalent Decimal | Equivalent BInary |
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 10 | 8 | 1000 |
| 9 | 11 | 9 | 1001 |
| A | 12 | 10 | 1010 |
| B | 13 | 11 | 1011 |
| C | 14 | 12 | 1100 |
| D | 15 | 13 | 1101 |
| E | 16 | 14 | 1110 |
| F | 17 | 15 | 1111 |
Hexadecimal to Octal Questions
Q.1: Find the equivalent octal form of C116.
Solution: Given, a hexadecimal number is C1
C116 = (C × 161) + (1 × 160)
= C × 16 + 1 × 1
=12 × 16 + 1
= 192 + 1
C116 =193 (Decimal form)
Now we have to convert this decimal to octal number;

The octal number is 3018
Hence, C116 = 3018
Q.2: Find the equivalent octal form of F16.
Solution: Given, a hexadecimal number is F.
F16 = (F × 160)
= F × 1
= F
= 15(Decimal form)
Now we have to convert this decimal to equivalent octal number;
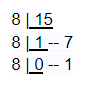
The octal number is 178
Hence, F16 = 178
Q.3: Find the equivalent octal form of 10516
Solution: Given, a hexadecimal number is 105.
10516 = (1 × 162) + (0 × 161) + (5 × 160)
= 1×256 + 0 × 16 + 5 × 1
=256 + 0 +5
= 261(Decimal form)
Now we have to convert this decimal to equivalent octal;

The octal number is 4058
Hence, 10516 = 4058
Practice Questions
- Convert ABCD16 to equivalent octal form.
- Convert 91216 to equivalent octal form.
- Convert 216 to equivalent octal form.
- Convert 1016 to equivalent octal form.