Curved Line
A “Curved line” or simply a ” Curve” is a line that is not straight. We see curves everywhere around us. Be it art or decoration or a general thing, and curves can be seen around us. In this article, we are going to learn the definition of a curved line, different types of curved lines with many examples.
What is a Curved Line?
A curved line is one that is not straight and is bent. Ideally, it is smooth and continuous. In other words, a curve is defined as a group of points that resemble a straight line that falls between two neighbouring points. We know that the curvature of the straight line is zero. Hence, if the curvature of a line is not zero, then we can call it a curved line. The following figure shows the different types of curved lines.
Difference Between Straight and Curved Line
| Straight Line | Curved Line |
| A straight line is the shortest line that joins any two points.
It always moves in one direction. |
A bent line that is not straight is called a Curved Line.
It doesn’t move in one direction. |
Examples of Curved Lines
There are many examples of curved lines like the alphabets – C and S. Whereas the letters A, M, N, L, etc are not examples of curves since they can be formed by joining the line segments (or straight lines).
Also, Read:
Different Types of Curved Lines
The curved lines can be classified into different types. They are:
- Simple Curve
- Non-simple Curve
- Algebraic Curve
- Transcendental Curve
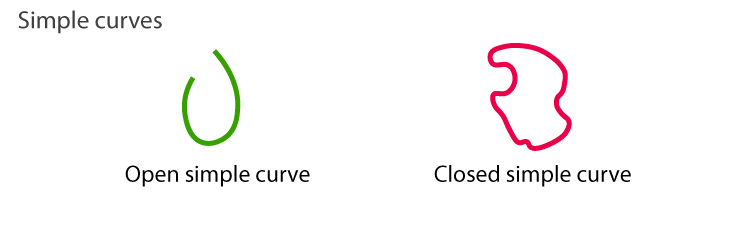
Simple Curve
A simple curve is defined as a curve that doesn’t cross itself. We know that the open curve has two endpoints whereas a closed curve has no endpoints. A closed curve creates a path that may begin from any point and terminate at the same point. Thus, the simple curve may be open or closed.
Non-simple Curve
The non-simple curve is a type of curve that intersects with itself while changing its direction. Like simple curves, the non-simple curves can also be open or closed.
Algebraic Curve
A plane curve where a set of points are located on the Euclidean plane and are represented in terms of polynomials is called Algebraic Curve. The polynomial’s degree denotes the degree of the curve.
C = {(a, b) ∈ R2: P(a, b) = 0}
Transcendental Curve
This curve is different from the algebraic curve. The curve that does not represent the algebraic form, then it is called a transcendental curve. This curve might have many intersecting points together with the straight line. Hence, a transcendental curve is not a polynomial based on a and b.
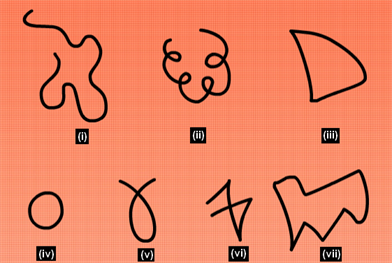
Practice Question
Question: Identify the open and closed curves from the below figure.
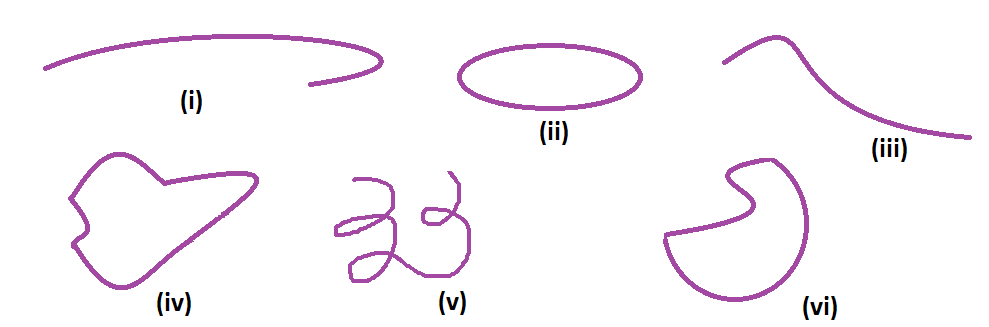
To learn more Maths-related concepts, stay tuned with BYJU’S – The Learning App and download the app today to learn all Maths concepts easily by exploring more videos.