Beta Distribution
The Beta distribution is a type of probability distribution which represents all the possible value of probability. Let us discuss its definition and formula with examples. In probability and statistics, the Beta distribution is considered as a continuous probability distribution defined by two positive parameters. It is a type of probability distribution which is used to represent the outcomes or random behaviour of proportions or percentage.
Why are Beta Distributions Used in Project Management?
The three-point technique, which is also called the beta distribution technique, is used to recognize the uncertainty in the estimated project time. It provides powerful quantitative tools to identify the tasks which are having the greatest risk. It also manages the time for project completion.
Table of contents:
Beta Distribution Definition
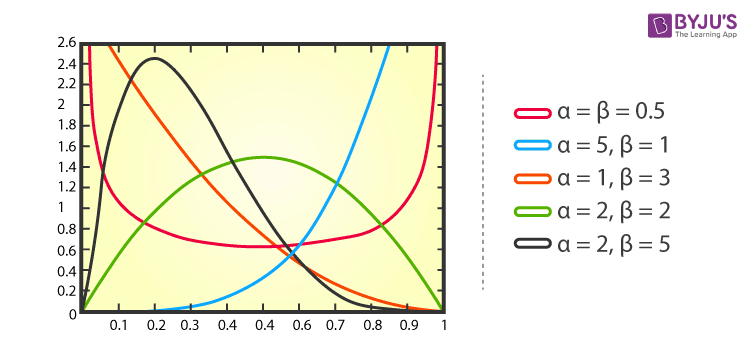
The beta distribution is a family of continuous probability distributions set on the interval [0, 1] having two positive shape parameters, expressed by α and β. These two parameters appear as exponents of the random variable and manage the shape of the distribution.
Usually, the basic distribution is known as the Beta distribution of its first kind, and prime beta distribution is called for its second kind.
The most common use of this distribution is to model the uncertainty about the probability of success of a random experiment. In project management, a three-point technique called “beta distribution” is used, which recognizes the uncertainty in the estimation of the project time. It provides powerful quantitative tools coupled with the basic statistics to compute the confidence levels for the expected completion time.
Also, the beta distribution is used in PERT where it produces a bell-shaped curve which is nearly normal. Consider an example; the beta distribution is used in the Bayesian Analysis to define the initial knowledge about the probability of the success that helps to complete the specified mission successfully. It is a suitable method for the random behaviour of the proportions and percentages.
Beta Distribution Notation
It is defined on the interval [0,1] denoted by α and β, usually. α and β are two positive parameters that appear as exponents of the random variable and is intended to control the shape of the distribution. Its notation is Beta(α,β), where α and β are the real numbers, and the values are more than zero.
Also, read:
Beta Distribution Formula
The beta distribution is used to check the behaviour of random variables which are limited to intervals of finite length in a wide variety of disciplines.
The characterization of this distribution is basically defined as Probability Density Function, Cumulative Density Function, Moment generating function, Expectations and Variance and its formulas are given below.

Properties
Some of the properties that satisfy the distribution are as follow:
The measure of central tendency. They are:
- Mean
- Median
- Mode
- Geometric Mean
- Harmonic Mean
The measure of statistical dispersion, such as:
- Variance
- Geometric variance and covariance
- Mean absolute difference
- Mean absolute deviation around the mean
Beta Distribution Applications
It is used in many applications, that includes
- Bayesian hypothesis testing
- The rule of succession
- Task duration modelling
- Project planning control systems like CPM and PERT.
Beta Distribution Example
Problem: Suppose, if in a basket there are balls which are defective with a Beta distribution of \(\alpha\)=5 and \(\beta\)=2 . Compute the probability of defective balls in the basket from 20% to 30%.
Solution: Let us consider the balls are defective with a Beta distribution of \(\alpha\)=2 and \(\beta\)=5. Now to calculate the probability of defective balls from 20% to 30% in the basket we have to apply the Beta probability density function formula, which is;
P(x) = \(x^{a-1}(1-x)^{\beta -1}/B(\alpha ,\beta )\)
P(0.2\(\leq\)x\(\leq\)0.3)= \(\sum_{0.2}^{0.3}x^{2-1}(1-x)^{5 -1}/B(2 ,5 )\)
=0.235185
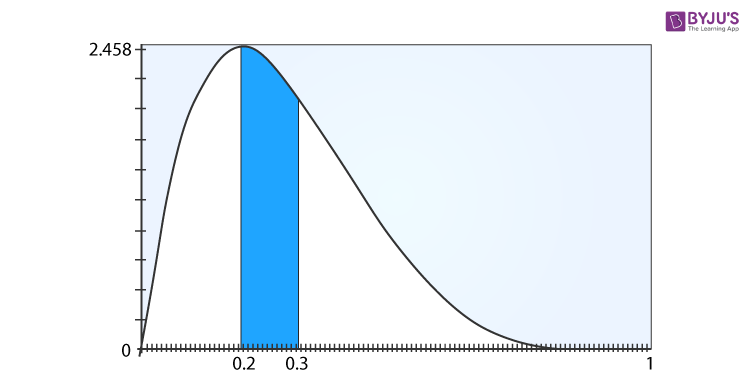
We hope with this example problem, the concept of beta distribution is understood.
Learn more on related Maths topics only on BYJU’S- The Learning App.
