Class 9 Maths Chapter 12 Heron’s Formula

Home → Class 9 Maths Chapter 12 Heron’s Formula

Class 9 Maths Chapter 12 Heron’s Formula MCQs are available online here, with solved answers. The MCQs are prepared as per the latest exam pattern for Class 9. The objective questions are prepared chapter-wise, as per the CBSE syllabus (2021-2022) and NCERT curriculum. These questions are provided with detailed explanations. Get Chapter-wise Class 9 Maths MCQs at BYJU’S.

Download the below PDF to get more MCQs on Class 9 Maths Chapter 12 Heron’s Formula.

Class 9 Maths Chapter 12 Heron’s Formula MCQs – Download PDF

MCQs on Class 9 Maths Chapter 12 Heron’s Formula

Choose the correct answer and solve the MCQs on Heron’s formula.

1) Area of the triangle is equal to:

a. Base x Height

b. 2(Base x Height)

c. ½(Base x Height)

d. ½ (Base + Height)

Answer: c

2) If the perimeter of an equilateral triangle is 180 cm. Then its area will be:

a. 900 cm²

b. 900√3 cm²

c. 300√3 cm²

d. 600√3 cm²

Answer: b

Explanation: Given, Perimeter = 180 cm

3a = 180 (Equilateral triangle)

a = 60 cm

Semi-perimeter = 180/2 = 90cm

Now as per Heron’s formula,

\(A = \sqrt{s(s-a)(s-b)(s-c)}\)

Hence, if we put the values here, we get:

A = 900√3

3) The sides of a triangle are 122 m, 22 m and 120 m respectively. The area of the triangle is:

a. 1320 sq.m

b. 1300 sq.m

c. 1400 sq.m

d. 1420 sq.m

Answer: a

Explanation: Given,

a = 122 m

b = 22 m

c = 120 m

Semi-perimeter, s = (122+22+120)/2 = 132 m

Using heron’s formula:

\(A = \sqrt{s(s-a)(s-b)(s-c)}\)

Put the values of s, a, b and c, to get the answer equal to 1320 sq.m.

4) The area of triangle with given two sides 18cm and 10cm, respectively and perimeter equal to 42 cm is:

a. 20√11 cm²

b. 19√11 cm²

c. 22√11 cm²

d. 21√11 cm²

Answer: d

Explanation: Perimeter = 42

a+b+c=42

18+10+c=42

c=42-28=14 cm

Semi perimeter, s = 42/2 = 21cm

Using Heron’s formula:

\(A = \sqrt{s(s-a)(s-b)(s-c)}\)

Put the values of s, a, b and c, to get the answer equal to 21√11 cm²

5) The sides of a triangle are in the ratio 12: 17: 25 and its perimeter is 540cm. The area is:

a. 1000 sq.cm.

b. 5000 sq.cm.

c. 9000 sq.cm.

d. 8000 sq.cm.

Answer: c

Explanation: The ratio of the sides is 12: 17: 25

Perimeter = 540 cm

Let the sides of the triangle be 12x, 17x and 25x.

Hence,

12x+17x+25x = 540 cm

54x = 540 cm

x = 10

Therefore,

a = 12x=12 x 10 = 120

b = 17x = 17 x 10 = 170

c = 25x = 25 x 10 = 250

Semi-perimeter, s = 540/2 = 270 cm

Putting the values of s, a, b and c in Heron’s formula, we will get the area equal to 9000 sq.cm.

6) The equal sides of the isosceles triangle are 12 cm, and the perimeter is 30 cm. The area of this triangle is:

a. 9√15 sq.cm

b. 6√15 sq.cm

c. 3√15 sq.cm

d. √15, sq.cm.

Answer: a

Explanation: Given,

Perimeter = 30cm

Semiperimeter, s = 30/2 = 15cm

a = b = 12cm

c=?

a+b+c = 30

12 +12+c=30

c=30-24 = 6cm

By putting the values of s, a, b and c in Heron’s formula, we can get the value of area.

7) A quadrilateral whose sides are 3cm, 4cm, 4cm, 5cm and one of the diagonal is equal to 5cm as per the below figure. The area of the quadrilateral is:

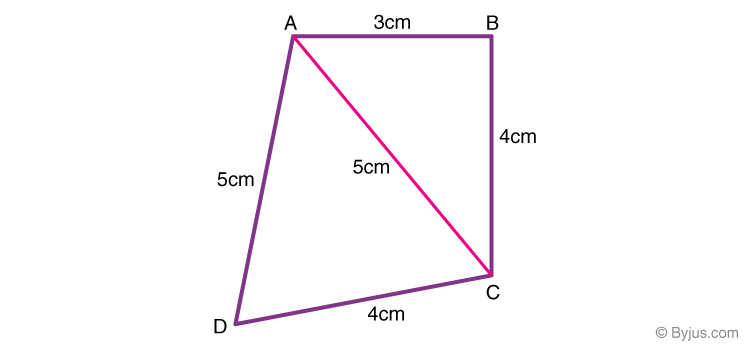
a. 19.17 sq.cm

b. 15.17 sq.cm

c. 20.17 sq.cm

d. 22.17 sq.cm.

Answer: b

Explanation: Using Pythagoras theorem, in ΔABC,

AC² = AB² + BC²

⇒ 5² = 3² + 4²

⇒ 25 = 25

Hence, ABC is a right triangle.

Area of ΔABC = ½ x 3 x 4 = 6 sq.cm

Semiperimeter of ΔACD = (5+5+4)/2 = 14/2 = 7cm

Area of ΔACD can be determined by using Heron’s formula.

Therefore, the area of quad.ABCD = Area of ΔABC + Area of ΔACD

8) The area of an equilateral triangle having side length equal to √3/4cm is:

a. 2/27 sq.cm

b. 2/15 sq.cm

c. 3√3/64 sq.cm

d. 3/14 sq.cm

Answer: c

Explanation: Here, a = b = c = √3/4

Find the semi-perimeter of the triangle and use Heron’s formula to find the answer.

9) The sides of a parallelogram are 100 m each and length of the longest diagonal is 160m. The area of a parallelogram is:

a. 9600 sq.m

b. 9000 sq.m

c. 9200 sq.m

d. 8800 sq.m

Answer: a

Explanation: The diagonal divides the parallelogram into two equivalent triangles. Hence, its area will be equal to the sum of the area of the two triangles.

Hence, we can determine the area of the two triangles using Heron’s formula.

10) The sides of a triangle are in the ratio of 3: 5: 7 and its perimeter is 300 cm. Its area will be:

a. 1000√3 sq.cm

b. 1500√3 sq.cm

c. 1700√3 sq.cm

d. 1900√3 sq.cm

Answer: b

Explanation: Take the reference of Q.No.5

11) The base of a right triangle is 8 cm and the hypotenuse is 10 cm. Its area will be

(a) 24 cm²

(b) 40 cm²

(d) 80 cm²

Answer: a

Explanation:

Given: Base = 8 cm and Hypotenuse = 10 cm

Hence, height = √[(10² – 8²) = √36 = 6 cm

Therefore, area = (½)×b×h = (½)×8×6 = 24cm².

12) The edges of a triangular board are 6 cm, 8 cm and 10 cm. The cost of painting it at the rate of 9 paise per cm² is

(a) Rs 2.00

(b) Rs 2.16

(d) Rs 3.00

Answer: b

Explanation:

Given: a = 6cm, b= 8cm, c = 10 cm.

s = (6+8+10)/2 = 12

Hence, by using Heron’s formula, we can write:

A = √[12(12-6)(12-8)(12-10)]= √[(12)(6)(4)(2)]= √576 = 24cm²

Therefore, the cost of painting at a rate of 9 paise per cm² = 24×9 paise = Rs. 2.16

13) An isosceles right triangle has area of 8 cm². The length of its hypotenuse is

(a) √32 cm

(b) √16 cm

(d) √24 cm

Answer: a

Explanation:

Given that area of isosceles triangle = 8 cm².

As the given triangle is isosceles triangle, let base = height = h

Hence,

(½)×h×h = 8

(½)h² =8

h²=16

h= 4 cm

Since it is isosceles right triangle, Hypotenuse² = Base²+Height²

Hypotenuse²= 4²+4²

Hypotenuse² = 3²

Hypotenuse = √32 cm

14) The area of an isosceles triangle having a base 2 cm and the length of one of the equal sides 4 cm, is

(a) √15 cm²

(b) √(15/2) cm²

(d) 4√15 cm²

Answer: a

Explanation:

Given that a = 2 cm, b= c = 4 cm

s = (2+4+4)/2 = 5

By using Heron’s formula, we get:

A =√[5(5-2)(5-4)(5-4)] = √[(5)(3)(1)(1)] = √15 cm².

15) The perimeter of an equilateral triangle is 60 m. The area is

(a) 10√3 m²

(b) 15√3 m²

(d) 100√3 m²

Answer: d

Explanation:

Given: Perimeter of an equilateral triangle = 60m

3a = 60 m (As the perimeter of an equilateral triangle is 3a units)

a = 20 cm.

We know that area of equilateral triangle = (√3/4)a² square units

A = (√3/4)20²

A = (√3/4)(400) = 100√3 cm².

16) The sides of a triangle are 35 cm, 54 cm and 61 cm, respectively. The length of its longest altitude

(a) 16√5 cm

(b) 10√5 cm

(d) 28 cm

Answer: c

Explanation:

Given: a =35 cm, b=54cm, c =61cm

s = (35+54+61)/2 = 75 cm.

Hence, by using Heron’s formula, A = √[75(75-35)(75-54)(75-61)] = √(882000) = 420√5 cm²

The area of triangle with longest altitude “h” is given as”

(½)×a×h = 420√5

(½)×35×h = 420√5

h= (840√5)/35 = 24√5 cm.

17) The sides of a triangle are 56 cm, 60 cm and 52 cm long. Then the area of the triangle is

(a) 1322 cm²

(b) 1311 cm²

(d) 1392 cm²

Answer: c

Explanation:

Since, all the sides of a triangle are given, we can find the area of a triangle using Heron’s formula.

Let a = 56 cm, b= 60 cm, c = 52 cm

s = (56+60+52)/2 = 84 cm.

Area of triangle using Heron’s formula, A = √[s(s-a)(s-b)(s-c)] square units

A = √[84(84-56)(84-60)(84-52)] = √(1806336) =1344 cm².

18) If the area of an equilateral triangle is 16√3 cm², then the perimeter of the triangle is

(a) 48 cm

(b) 24 cm

(d) 36 cm

Answer: b

Explanation:

Given: Area of equilateral triangle = 16√3 cm²

(√3/4)a² = 16√3

a² = [(16√3)(4)]/√3

a² = 64

a = 8cm
Therefore, perimeter = 3(8) = 24 cm.

19) The area of an equilateral triangle with side 2√3 cm is

(a) 5.196 cm²

(b) 0.866 cm²

(d) 1.732 cm²

Answer: a

Explanation:

Given: Side = 2√3 cm

We know that, area of equilateral triangle = (√3/4)a² square units

A = (√3/4)(2√3)² = (√3/4)(12) = 3√3 = 3(1.732) = 5.196 cm².

20) The length of each side of an equilateral triangle having an area of 9√3 cm² is

(a) 8 cm

(b) 36 cm

(d) 6 cm

Answer: d

Explanation:

Given: Area of equilateral triangle = 9√3 cm²

Hence, (√3/4)a² = 9√3

a² = [(9√3)(4)]/√3

a² = 36

a = 6cm.

Heron’s Formula
Maths Formulas for Class 9
Important Questions for Class 9 Maths
Heron’s Formula Class 9 Notes: Chapter 12
Important Questions Class 9 Maths Chapter 12-Heron’s Formula
CBSE Class 9 Maths Examination 2018: Important 3 marks questions

Stay tuned with BYJU’S – The Learning App and download the app today to get more class-wise concepts.

Class 9 Maths Chapter 12 Heron’s Formula

Trigonometry

Class 9 Maths Chapter 12 Heron’s Formula

MCQs on Class 9 Maths Chapter 12 Heron’s Formula

Related Articles