Binomial Theorem For Positive Integral Indices
Before understanding about Binomial Theorem, let us focus on what we have learnt about the expansions.
We all know the expansion of \( (a+b)^2, (a+b)^3, (a-b)^2, (a-b)^3\)
\((a+b)^2\)=\(a^2+2ab+b^2\)
\((a+b)^3\)=\(a^3+3a^2 b+3ab^2+b^3\)
(\(a-b)^2\)=\(a^2-2ab+b^2\)
\((a-b)^3\)=\(a^3-3a^2 b+3ab^2-b^3\)
Using the above expansions, we can easily find out the values of,
\((105)^2\)=\((100+5)^2\)
=\(100^2+2×100×5+5^2\)
=\(10000 + 1000 + 25\) = \( 11025\)
Similarly,
\((101)^3\)=\((100+1)^3\)
=\( 100^3 + 3 × 100^2 × 1 + 3 × 100 × 1^2 + 1^3\)
\(1000000 + 30000 + 300 + 1\) = \( 1030301 \)
But, finding out the values of \((102)^6\), \((99)^5 \) with repeated multiplication is difficult. This is made easy with a theorem known as binomial theorem.
Binomial Theorem for Positive Integral Indices Statement
The theorem states that “the total number of terms in the expansion is one more than the index. For example, in the expansion of (a + b)n, the number of terms is n+1 whereas the index of (a + b)n is n, where n be any positive integer.
By using this theorem, we can expand \((a+b)^n\), where n can be a rational number. Binomial theorem for positive integral indices is discussed here.
Let us write the expansion of \((a+b)^n \) , [0≤n≤5 and n is an integer] and find the properties of binomial expansion.
\((a+b)^0\)=\(1\)
\((a+b)^1\)=\((a+b)\)
\((a+b)^2\)=\(a^2+2ab+b^2\)
\((a+b)^3\)=\(a^3+3a^2 b+3ab^2+b^3\)
\((a+b)^4\)=\(a^4+4a^3 b+6a^2 b^2+4ab^3+b^4\)
\((a+b)^5\)=\(a^5+5a^4 b+10a^3 b^2+10a^2 b^3+5ab^4 +b^5\)
Properties of the Binomial Theorem for positive Integrals Index
- If you notice the power of a and b, exponent of a [first quantity] is decreasing by 1 in the successive terms. Meanwhile, exponent of b is increasing by 1 in the successive terms.
For example; in the expansion of \( (a+b)^3 \) = \( a^3+3a^2 b+3ab^2+b^3\)In the first term \( a^3\) , exponent of a is 3 and exponent of b is 0.In the second term3\(a^2\) b, exponent of a is 2 and exponent of b is 1.In the third term \(3ab^2\), exponent of a is 1 and exponent of b is 2.In the fourth term \(b^3\), exponent of a is 0 and exponent of b is 3.
- The total number of terms in the expansion is one more than the exponent or index of (a+b).For example; in the expansion of \((a+b)^4\)=\(a^4+4a^3 b+6a^2 b^2+4ab^3+b^4\)Index of (a+b) is 4 and the number of terms in the expansion is 5.
- The exponent or index of (a+b) will be equal to the sum of exponents of a and b in each term of the expansion.
We will see the relation between the index of (a+b)and the coefficients of the terms in the expansion.
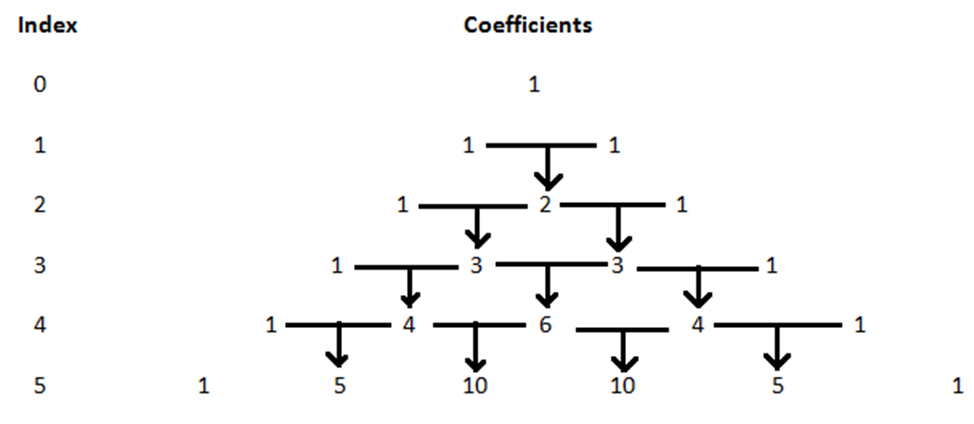
Index Coefficients
0 1
1 1 1
2 1 2 1
3 1 3 3 1
4 1 4 6 4 1
5 1 5 10 10 5 1
- The coefficients of the first term and last term of the expansion \((a+b)^n\) [where n can be any integer] is 1
- Adding the 1’s of the index 1 gives you the 2 for the index 2.
Similarly, adding 1 and 2 of the index 2 gives you the 3’s of the index 3.
Refer the following figure for better understanding.
The discussion above is a brief introduction to binomial theorem for positive integral indices. To learn more about binomial expansion, log onto www.byjus.com and fall in love with BYJU’s way of learning.’