In Probability and Statistics, the Cumulative Distribution Function (CDF) of a real-valued random variable, say “X”, which is evaluated at x, is the probability that X takes a value less than or equal to the x. A random variable is a variable that defines the possible outcome values of an unexpected phenomenon. It is defined for both discrete and random variables. It is also used to specify the distribution of the multivariate random variables. If the random variable is above a particular level, it is known as tail distribution or the Complementary Cumulative Distribution Function (CCDF). In this article, you will understand what cumulative distribution function is, its properties, formulas, applications and examples.

Table of Contents:

• Definition
• Formula
• Properties
• Cumulative Frequency Distribution
• Applications
• Example

What is a Cumulative Distribution Function?

The Cumulative Distribution Function (CDF), of a real-valued random variable X, evaluated at x, is the probability function that X will take a value less than or equal to x. It is used to describe the probability distribution of random variables in a table. And with the help of these data, we can easily create a CDF plot in an excel sheet.

In other words, CDF finds the cumulative probability for the given value. To determine the probability of a random variable, it is used and also to compare the probability between values under certain conditions. For discrete distribution functions, CDF gives the probability values till what we specify and for continuous distribution functions, it gives the area under the probability density function up to the given value specified.

Cumulative Distribution Function Formula

The CDF defined for a discrete random variable and is given as

F_{x(x) = P(X ≤ x)}

Where X is the probability that takes a value less than or equal to x and that lies in the semi-closed interval (a,b], where a < b.

Therefore the probability within the interval is written as

P(a < X ≤ b) = F_x(b) – F_x(a)

The CDF defined for a continuous random variable is given as;

Here, X is expressed in terms of integration of its probability density function f_x.

In case, if the distribution of the random variable X has the discrete component at value b,

P(X = b) = F_x(b) – lim_x→b- F_x(x)

Cumulative Distribution Function Properties

The cumulative distribution function F_x(x) of a random variable has the following important properties:

• Every CDF F_x is non decreasing and right continuous

              lim_x→-∞F_x(x) = 0 and lim_x→+∞F_x(x) = 1

• For all real numbers a and b with continuous random variable X, then the function f_x is equal to the derivative of F_x, such that
  

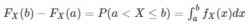
• If X is a completely discrete random variable, then it takes the values x₁, x₂, x₃,…  with probability p_i = p(x_i), and the CDF of X will be discontinuous at the points x_i:

FX(x) = P(X ≤ x) = \(\sum_{x_i\le x}P(X = x_i)=\sum_{x_i\le x}p(x_i)\)

This function is defined for all real values, sometimes it is defined implicitly rather than defining it explicitly. The CDF is an integral concept of PDF ( Probability Distribution Function )

Consider a simple example for CDF which is given by rolling a fair six-sided die, where X is the random variable

We know that the probability of getting an outcome by rolling a six-sided die is given as:

Probability of getting 1 = P(X≤ 1 ) = 1 / 6

Probability of getting 2 = P(X≤ 2 ) = 2 / 6

Probability of getting 3 = P(X≤ 3 ) = 3 / 6

Probability of getting 4 = P(X≤ 4 ) = 4 / 6

Probability of getting 5 = P(X≤ 5 ) = 5 / 6

Probability of getting 6 = P(X≤ 6 ) = 6 / 6 = 1

From this, it is noted that the probability value always lies between 0 and 1 and it is non-decreasing and right continuous in nature.

Cumulative Frequency Distribution

The set of data represented in a tabular or graphical form, showing the frequency of observations occurring in a given interval, is the frequency distribution. In the case of cumulative frequency, the number of observations that occur beyond any specific observation is calculated. To learn in detail, visit the article for cumulative frequency distribution and understand the concept thoroughly with the help of examples.

Cumulative Distribution Function Applications

The most important application of cumulative distribution function is used in statistical analysis. In statistical analysis, the concept of CDF is used in two ways.

• Finding the frequency of occurrence of values for the given phenomena using cumulative frequency analysis.
• To derive some simple statistics properties, by using an empirical distribution function, that uses a formal direct estimate of CDFs.

Cumulative Distribution Function Example

Question:

The random variable with PDF is given by:

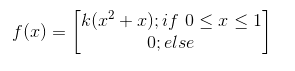
Find the cumulative distribution function(CDF)

Solution: The random variable with Probability Distribution Function is given to us. Let is find the CDF now;

For more information about mathematics articles, solved problems and video tutorials register with BYJU’S – The Learning App.