Class 9 Maths Chapter 7 Triangles MCQs are provided here with answers, online. All the MCQs are prepared as per the latest exam pattern. Students can practice these objective questions to score good marks in the final exam. All the problems here are based on the CBSE syllabus (2021-2022) and the NCERT curriculum. A detailed explanation is given for each question to help students understand the concepts. Learn chapter-wise MCQs, only at BYJU’S. Also, check Important Questions for Class 9 Maths.

MCQs on Class 9 Maths Chapter 7 Triangles

Solve the MCQs given below and choose the correct answer among the four options. Match your answers with the given answers here.

1) In triangle ABC, if AB=BC and ∠B = 70°, ∠A will be:

a. 70°

b. 110°

c. 55°

d. 130°

Answer: c

Explanation: Given,

AB = BC

Hence, ∠A=∠C

And ∠B = 70°

By angle sum property of triangle we know:

∠A+∠B+∠C = 180°

2∠A+∠B=180°

2∠A = 180-∠B = 180-70 = 110°

∠A = 55°

2) For two triangles, if two angles and the included side of one triangle are equal to two angles and the included side of another triangle. Then the congruency rule is:

a. SSS

b. ASA

c. SAS

d. None of the above

Answer: b

3) A triangle in which two sides are equal is called:

a. Scalene triangle

b. Equilateral triangle

c. Isosceles triangle

d. None of the above

Answer: c

4) The angles opposite to equal sides of a triangle are:

a. Equal

b. Unequal

c. supplementary angles

d. Complementary angles

Answer: a

5) If E and F are the midpoints of equal sides AB and AC of a triangle ABC. Then:

a. BF=AC

b. BF=AF

c. CE=AB

d. BF = CE

Answer: d

Explanation: AB and AC are equal sides.

AB = AC (Given)

∠A = ∠A (Common angle)

AE = AF (Halves of equal sides)

∆ ABF ≅ ∆ ACE (By SAS rule)

Hence, BF = CE (CPCT)

6) ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB, respectively. Then:

a. BE>CF

b. BE<CF

c. BE=CF

d. None of the above

Answer: c

Explanation:

∠A = ∠A (common arm)

∠AEB = ∠AFC (Right angles)

AB = AC (Given)

∴ ΔAEB ≅ ΔAFC

Hence, BE = CF (by CPCT)

7) If ABC and DBC are two isosceles triangles on the same base BC. Then:

a. ∠ABD = ∠ACD

b. ∠ABD > ∠ACD

c. ∠ABD < ∠ACD

d. None of the above

Answer: a

Explanation: AD = AD (Common arm)

AB = AC (Sides of isosceles triangle)

BD = CD (Sides of isosceles triangle)

So, ΔABD ≅ ΔACD.

∴ ∠ABD = ∠ACD (By CPCT)

8) If ABC is an equilateral triangle, then each angle equals to:

a. 90°

B.180°

c. 120°

d. 60°

Answer: d

Explanation: Equilateral triangle has all its sides equal and each angle measures 60°.

AB= BC = AC (All sides are equal)

Hence, ∠A = ∠B = ∠C (Opposite angles of equal sides)

Also, we know that,

∠A + ∠B + ∠C = 180°

⇒ 3∠A = 180°

⇒ ∠A = 60°

∴ ∠A = ∠B = ∠C = 60°

9) If AD is an altitude of an isosceles triangle ABC in which AB = AC. Then:

a. BD=CD

b. BD>CD

c. BD<CD

d. None of the above

Answer: a

Explanation: In ΔABD and ΔACD,

∠ADB = ∠ADC = 90°

AB = AC (Given)

AD = AD (Common)

∴ ΔABD ≅ ΔACD (By RHS congruence condition)

BD = CD (By CPCT)

10) In a right triangle, the longest side is:

a. Perpendicular

b. Hypotenuse

c. Base

d. None of the above

Answer: b

Explanation: In triangle ABC, right-angled at B.

∠B = 90

By angle sum property, we know:

∠A + ∠B + ∠C = 180

Hence, ∠A + ∠C = 90

So, ∠B is the largest angle.

Therefore, the side (hypotenuse) opposite to the largest angle will be the longest one.

11) Which of the following is not a criterion for congruence of triangles?

(a) SAS

(b) ASA

(c) SSA

(d) SSS

Answer: c

Explanation:

SSA is not a criterion for the congruence of triangles. Whereas SAS, ASA and SSS are the criteria for the congruence of triangles. 

12) In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are

(a) Isosceles and congruent

(b) Isosceles but not congruent

(c) Congruent but not isosceles

(d) Neither congruent nor isosceles

Answer: b

Explanation: 

Consider two triangles, ABC and PQR. If the sides AB = AC and ∠C = ∠P and ∠B = ∠Q, then the two triangles are said to be isosceles, but they are not congruent.

13) In ∆ PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is

(a) 2 cm

(b) 2.5 cm

(c) 4 cm

(d) 5 cm

Answer: c

Explanation:

Given that, in a triangle PQR, ∠R = ∠P.

Since, ∠R = ∠P, the sides opposite to the equal angles are also equal.

Hence, the length of PQ is 4 cm.

14) If AB = QR, BC = PR and CA = PQ, then

(a) ∆ PQR ≅ ∆ BCA

(b) ∆ BAC ≅ ∆ RPQ

(c) ∆ CBA ≅ ∆ PRQ

(d) ∆ ABC ≅ ∆ PQR

Answer: c

Explanation:

Consider two triangles ABC and PQR.

Given that, AB = QR, BC = PR and CA = PQ.

By using Side-Side-Side (SSS rule),

We can say, ∆ CBA ≅ ∆ PRQ.

15) If ∆ ABC ≅ ∆ PQR, then which of the following is not true?

(a) AC = PR 

(b) BC = PQ

(c) QR = BC

(d) AB = PQ

Answer: b

Explanation:

Given that, ∆ ABC ≅ ∆ PQR

Hence, AB = PQ

BC = QR

AC =PR

Thus, BC = PQ is not true, if ∆ ABC ≅ ∆ PQR.

16) In ∆ ABC, BC = AB and ∠B = 80°. Then ∠A is equal to

(a) 40°

(b) 50°

(c) 80°

(d) 100°

Answer: b 

Explanation: In a triangle, ABC, BC = AB and ∠B = 80°.

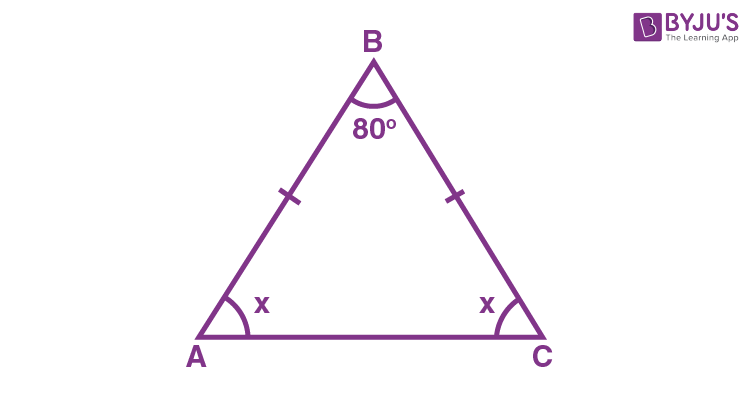
Thus, the given triangle is an isosceles triangle.

By using the angle sum property of a triangle, we get

x +  80°+x = 180°

2x+ 80°= 180°

2x = 180°- 80°

2x = 100°

x = 100°/2 = 50°

Therefore, ∠A = 50°.

17) Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be

(a) 3.4 cm

(b) 3.6 cm

(c) 3.8 cm

(d) 4.1 cm

Answer: a

Explanation: If two sides of a triangle are of lengths 5 cm and 1.5 cm, then the length of the third side of the triangle cannot be 3.4 cm. Because the difference between the two sides of a triangle should be less than the third side.

18) In ∆ ABC, AB = AC and ∠B = 50°. Then ∠C is equal to

(a) 40°

(b) 50°

(c) 80°

(d) 130°

Answer: b

Explanation:

Given that, in a triangle ABC, AB = AC and ∠B = 50°.

Since the given triangle is an isosceles triangle, the angles opposite to the equal sides are also equal. Hence, ∠C = 50°.

19) In ∆ PQR, if ∠R > ∠Q, then

(a) QR < PR 

(b) PQ < PR

(c) PQ > PR

(d) QR > PR 

Answer: c

Explanation: In a triangle PQR, if ∠R > ∠Q, then PQ > PR, because the side opposite to the greater angle is longer.

20) It is given that ∆ ABC ≅ ∆ FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true? 

(a) DF = 5 cm, ∠F = 60°

(b) DF = 5 cm, ∠E = 60° 

(c) DE = 5 cm, ∠E = 60°

(d) DE = 5 cm, ∠D = 40

Answer: b

Explanation:

Given that, ∆ ABC ≅ ∆ FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°.

By using the CPCT rule, 

DF = 5 cm, since AB = 5 cm.

Again by using CPCT rule, ∠E = ∠C.

Therefore, ∠E = ∠C = 180° – (∠A+ ∠B) [ By using angle sum property of triangle]

∠E = 180° – (80°+ 40°)

∠E = 180° – 120°

∠E = 60°

Related Articles for Class 9

• Areas Of Parallelograms And Triangles Class 9 Notes: Chapter 9
• Class 9 Maths Chapter 9 Areas of Parallelogram and Triangles MCQs
• Congruence of Triangles Class 9
• Important Questions Class 9 Maths Chapter 7- Triangles
• Important Questions Class 9 Maths Chapter 9-Areas of Parallelograms & Triangles

Stay tuned with BYJU’S – The Learning App and download the app today to get more class-wise concepts.