Congruence of Triangles Class 9
Congruence of triangles class 9 helps the students to understand the concept of congruence in a different perspective. It states that that two triangles are said to be congruent if they are copies of each other and when superposed, they cover each other exactly. In other words, two triangles are congruent if the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle. Congruence of triangles class 9 helps the students to learn about some of the axiom rules that every student should be needed to know for proceeding their higher studies.
Assume the triangle ABC and PQR
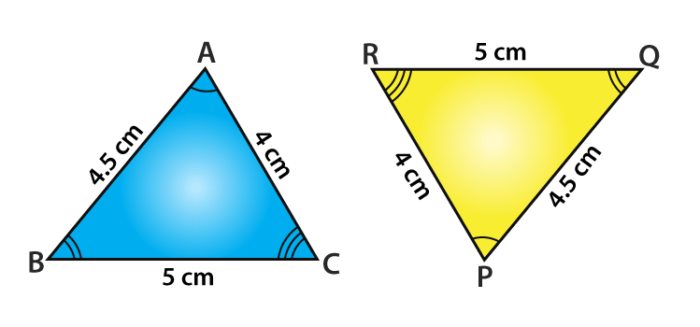
If a triangle PQR is congruent to a triangle ABC, we write it as ∆ PQR ≅ ∆ ABC.
Note that when ∆ PQR ≅ ∆ ABC, then sides of ∆ PQR fall on corresponding equal sides of ∆ ABC and so is the case for the angles.
This means that PQ covers AB, QR covers BC and RP covers CA;
∠P, ∠Q and ∠R covers ∠A, ∠B and ∠C respectively.
Also, between the vertices, there is an existence of one-one correspondence.
That is, P corresponds to A, Q corresponds to B, R corresponds to C and it is written as
\(P\leftrightarrow A, Q\leftrightarrow B, R\leftrightarrow C\)Under this condition, the correspondence ∆ PQR ≅ ∆ ABC is true but is not correct for the correspondence ∆QRP ≅ ∆ ABC.
Congruence of Triangles Criterion
The criteria for congruence of triangles class 9 is explained using two axiom rules.
SSS Congruence Rule (Side – Side – Side)
Two triangles are said to be congruent if all the sides of a triangle are equal to all the corresponding sides of another triangle.
SAS Congruence Rule (Side – Angle – Side)
Two triangles are said to be congruent if two sides and the included angle of one triangle are equal to the two sides and the included angle of the other triangle.
Proof :
In the given figure OA = OB and OD = OC.
Show that
(i) ∆ AOD ≅ ∆ BOC and (ii) AD || BC.
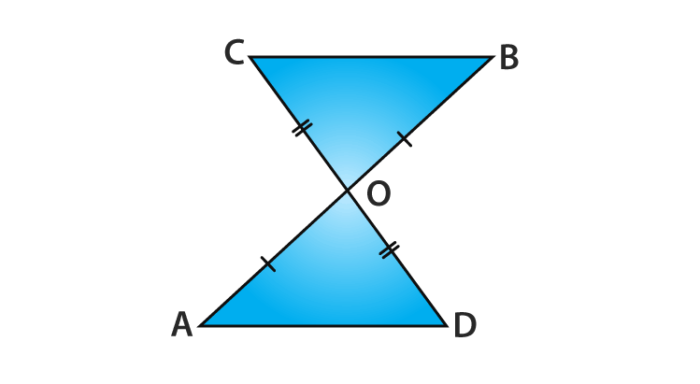
Solution :
(i) You may note that in triangle AOD and triangle BOC,
Given data are: OA = OB and OC = OD
Also, ∠AOD and ∠BOC form a pair of vertically opposite angles, we may write as
∠AOD = ∠BOC.
So, we get ∆ AOD ≅ ∆ BOC (Using the SAS congruence rule)
(ii) In congruent triangles, AOD and BOC, the corresponding parts of the triangle sides are also equal.
So, we get ∠ OAD = ∠ OBC and these conditions form a pair of alternate angles for line segments AD and BC.
Therefore, the sides AD || BC.
Hence, proved.
For More Information On SAS And ASA Congruency Rules, Watch The Below Video:

ASA Congruence Rule ( Angle – Side – Angle )
Two triangles are said to be congruent if two angles and the included side of one triangle are equal to two angles and the included side of another triangle.
Proof :
From the given two triangles, ABC and DEF in which:
∠B = ∠E, and ∠C = ∠F and the BC = EF
To prove that ∆ ABC ≅ ∆ DEF
For proving congruence of the two triangles, the three cases involved are
Case (i): Let AB = DE

You will observe that
AB = DE (Assumed)
Given ∠B = ∠E and BC = EF
So, from SAS Rule we get, ∆ ABC ≅ ∆ DEF
Case (ii): Let it possible the side AB > DE. Now take a point P on AB such that it becomes
PB = DE.
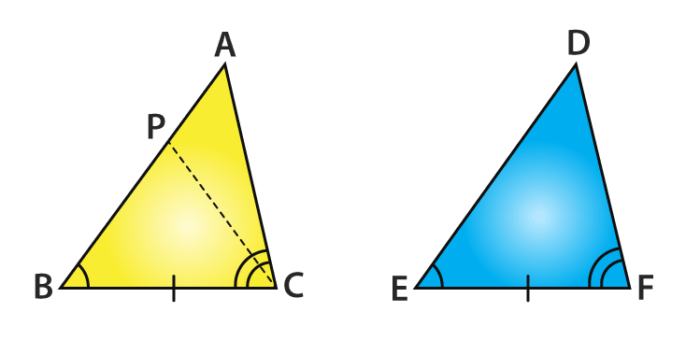
Now consider ∆ PBC and ∆ DEF,
IT is noted that in triangle PBC and triangle DEF,
From construction, PB = DE
Given,∠ B = ∠ E
BC = EF
So, we conclude that, from the SAS congruence axiom
∆ PBC ≅ ∆ DEF
Since the triangles are congruent, their corresponding parts of the triangles are also equal.
So, ∠PCB = ∠DFE
But, we are provided with that
∠ACB = ∠DFE
So, we can say ∠ACB = ∠PCB
Is this condition possible?
This condition is possible only if P coincides with A or when BA = ED
So, ∆ ABC ≅ ∆ DEF (From SAS axiom)
Case (iii): If AB < DE, we can take a point M on DE such that it becomes ME = AB and
repeating the arguments as given in Case (ii), we can conclude that AB = DE and so we get
∆ ABC ≅ ∆ DEF.
Suppose now consider that in two triangles, two pairs of angles and one pair of corresponding
sides are equal but the side of a triangle is not included between the corresponding equal pairs of angles. Can you say that the triangles still congruent? Absolutely, You will notice that they are congruent. Because the sum of the three angles of a triangle is 180°. If two pairs of
angles are equal, the third pair of angles are also equal. It is called as AAS congruence rule when two triangles are congruent if any two pairs of angles and one pair of corresponding sides are equal.
For More Information On Introduction To Congruent Triangles, Watch The Below Video:

Congruence of Triangles Example Problem
Question :
Line segment AB is parallel to the line-segment CD. From the given figure, O is the midpoint of AD. Show that (1) ∆AOB ≅ ∆DOC
(2) O is also the midpoint of BC.
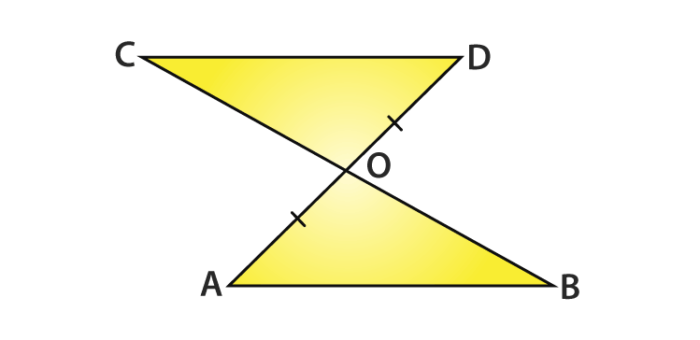
Solution:
(i) Consider a triangle AOB and triangle DOC.
You can write it as ∠ ABO = ∠ DCO
Since BC is the transversal and the alternate angles as AB || CD
Noted from, vertically opposite angles ∠ AOB = ∠ DOC
Given : OA = OD
Therefore, from AAS rule, ∆AOB ≅ ∆DOC
(ii) From Corresponding Parts of Congruent Triangles(CPCT)
It is observed that OB = OC
So, O is the midpoint of BC.
Hence Proved.
Visit BYJU’S – The Learning App for more information on congruence of triangles class 9 and other maths-related articles and also watch interactive videos to learn the concepts with ease.
| Related Links | |
| Types Of Angles | Lines and Angles Introduction |
| Line | Angle Relationships: Parallel Lines & Transversal |