In differential calculus, the chain rule is a formula used to find the derivative of a composite function. If y = f(g(x)), then as per chain rule the instantaneous rate of change of function ‘f’ relative to ‘g’ and ‘g’ relative to x  results in an instantaneous rate of change of ‘f’ with respect to ‘x’. Hence, the derivative of y will be given as, y’ = f'(g(x)).g'(x). Chain rule is one of the important rules in differentiation. In this article, we will learn the chain rule formula with solved examples. 

What is Chain Rule?

The rule applied for finding the derivative of the composite function (e.g. cos 2x, log 2x, etc.) is basically known as the chain rule. It is also called the composite function rule. The chain rule is applicable only for composite functions. So before starting the formula of the chain rule, let us understand the meaning of composite function and how it can be differentiated.

Composite Function For Chain Rule

A composite function is denoted as:

(fog)(x) = f(g(x))

Suppose f(x) and g(x) are two differentiable functions such that the derivative of a composite function f(g(x)) can be expressed as

(fog)′ = (f′o g) × g′

This can be understood in a better way from the example given below:

Consider f(x) = e^{x2 + 4} and g(x) = x² + 4

Therefore, f'(x) = 2x e^x2 and g'(x) = 2x

Now, the derivative of composite function of f(x) and g(x) can be written as:

(fog)′  = (f′o g) × g′

Let  g(x) = k then f(x) = e^k {where k = x² + 4}

⇒ (f′o g)  = e^k and g′ = 2x

⇒(fog)′  = e^k × 2x = e^{x2 + 4}  × 2x

Click here to learn more about composition of functions.

Chain Rule in Differentiation

Let f represent a real valued function which is a composition of two functions u and v such that:

f = v(u(x))

Let us assume u(x) = t

Now if the functions u and v are differentiable and dt/dx and dv/dt exist, then the composite function f(x) is also differentiable. This can be done as given below.

Using Leibnitz notation, we can express the differentiation of the above function as

df/dx = (dv/dt) × (dt/dx)

As the name suggests, chain rule means differentiating the terms one by one in a chain form, starting from the outermost function to the innermost function. In layman terms, to differentiate a composite function at any point in its domain, first differentiate the outer part (i.e. the function enclosing some other function) and then multiply it with the inner function’s derivative function. This will provide us with the desired differentiation.

Chain Rule Formula

The formula of chain rule for the function y = f(x), where f(x) is a composite function such that x = g(t), is given as:

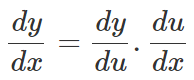
This is the standard form of chain rule of differentiation formula.

Another formula of chain rule is represented by:

y’ = d/dx ( f(g(x) ) = f’ (g(x)) · g’ (x)

Let us illustrate this rule with the help of an example:

Example: Find the derivative of the function f(x) = sin(2x² – 6x).

Solution: 

The given can be expressed as a composite function as given below:

f(x) = sin(2x² – 6x)

u(x) =2x² – 6x

v(t) = sin t

Thus, t = u(x) = 2x² – 6x

⇒f(x) = v(u(x))

According to the chain rule,

df(x)/dx = (dv/dt) × (dt/dx)

Where,

dv/dt = d/dt (sin t) = cos t

dt/dx = d/dx [u(x)] = d/dx (2x² – 6x) = 4x – 6

Therefore, df/dx = cos t × (4x – 6)

= cos(2x² – 6x) × (4x – 6)

= (4x – 6) cos(2x² – 6x)

Related Articles

• Differentiation
• Quotient Rule
• Product Rule
• Differentiation Formulas
• Derivative of a Function
• Differential Calculus

Chain Rule Solved Examples

Question 1:

Find the derivative of the function given by \(f(x)\) = \(sin(e^{x^3})\)

Solution:

Given,

\(f(x)\) = \(sin(e^{x^3})\)

It is a composition of three functions such as:

p(s) = sin s, q(t) = e^t and r(x) = x³

Thus, f(x) = p(q(r(x)))

That means, t = x³ and s = e^x3

Using chain rule formula,

df/dx = (dp/ds) × (ds/dt) × (dt/dx)

= [d/ds (sin s)] × [d/dt (e^t)] × [d/dx (x³)]

= cos s × e^t × 3x²

= \(cos e^{x^3} × e^{x^3} × 3x^2\)

Question 2:

Find the derivative of the function given by \( f(x) \) = \( \sqrt{tan (x^2 + 1)}\)

Solution:

Given,

\( f(x) \) = \( \sqrt{tan (x^2 + 1)}\)

The given function represents a composition of functions where

\(f(x)\) = \(\sqrt{tan (x^2 + 1)}\)

\( u(x) \)= \(x^2 + 1\)

\( v(t) \) =\( \sqrt{tan t}\)

\(\Rightarrow f(x)\) =\( v(u(x)) \)

According to the chain rule,

\(\frac{df}{dx}\) = \(\frac{dv}{dt}\) × \(\frac{dt}{dx}\)

\(\Rightarrow \frac{dv}{dt}\) =\( \frac{1}{2} (tan t)^{\frac{-1}{2}}× sec^2 t\)
=\( \frac{1}{2} × \frac{1}{\sqrt{tan t}} × sec^2 t\)

Also \(t\) = \(u(x)\)

\(\Rightarrow \frac{dt}{dx} \)= \(2x\)

\(\Rightarrow \frac{df}{dx}\) =\( 2x × \frac{1}{2} × \frac{1}{\sqrt{tan t}} × sec^2 t\)

Therefore,

\(\frac{df}{dx}\) = \(\frac{x sec^2(x^2 + 1)}{\sqrt{tan(x^2 + 1)}}\)

Chain Rule for Partial Derivatives

The chain rule for total derivatives implies a chain rule for partial derivatives. We know that the partial derivative in the ith coordinate direction can be evaluated by multiplying the ith basis vector’s Jacobian matrix when the total derivative exists. Hence, the chain rule for the function y = f(u) = (f₁(u), …, f_k(u)) and u = g(x) = (g₁(x), …, g_m(x)) can be written for partial derivatives as:

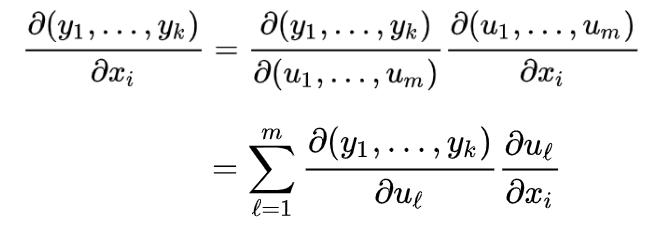
Chain Rule Practice Problems

Practice the question given below:

1. Find the derivative of the function y = cos²(x⁴)
2. Using chain rule, find the derivative of y = sin⁴x + sin x⁴
3. Find the derivative of y = 2 ln[ln(ln sec x)]

To practice more on chain rule and differentiation of composite functions,  download BYJU’S – The Learning App to excel in knowledge.