Circles class 9 – The collection of all points equidistant from a fixed point in a plane is called a circle. Let us discuss in detail about the definitions and terminologies used in a concept of the circle.

Circles Class 9 Notes

• A plane is divided by the circle into 3 parts, namely, the interior and exterior of the circle and the circle itself.
• A chord is a line passing from one point to another on the circumference of a circle.
• Diameter is a chord that passes through the centre.
• The perimeter of a circle is known as the circumference.
• Chords equal in length subtend equal angles at centre. Similarly, the chords are equal if the angles subtended by chords are equal at the centre.
• The perpendicular drawn on a chord from centre bisects the chord. Similarly, the line is perpendicular if it is drawn from the centre to bisects the chord.
• Only one circle can pass through 3 non-collinear points.
• Chords equal in length are equidistant from the centre. Similarly, Chords are equal if they are equidistant from the centre.
• In a cyclic quadrilateral, the sum of pair of angles opposite to each other is 180 degree.
• Angles subtended by the same line segment are equal.
• If chords of a circle are equal in length, then the corresponding arcs will be congruent. Similarly, if arcs are congruent, then the corresponding chords will be equal.

Circles Class 9 Examples

Example 1: 

An arc of a circle is given. Complete the circle.

Solution:

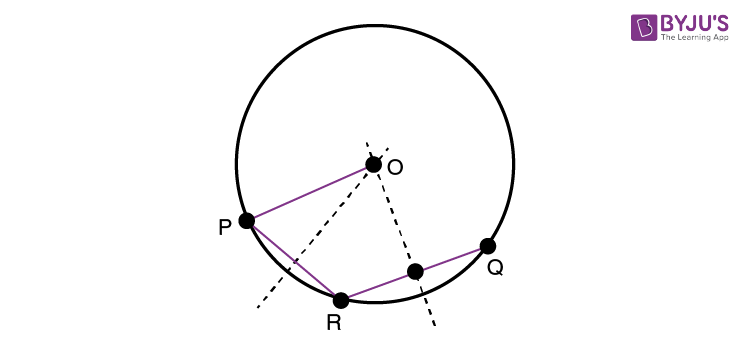
Let assume that PQ is the given arc of a circle. Now, we have to complete the circle for the given arc. It means that we need to find the radius and the centre point of a circle. 

Now, take the point R on the circle, and join the points PR and RQ. Now, by using the theorem: “There is one and only one circle passing through the three given non-collinear points”. Now, construct a circle based on this theorem to find the centre and radius. After obtaining the radius and centre, complete the circle for the given arc.

Example 2: 

Prove that the chords are equal if two intersecting chords of a circle make equal angles with the diameter passing through their point of intersection.

Solution:

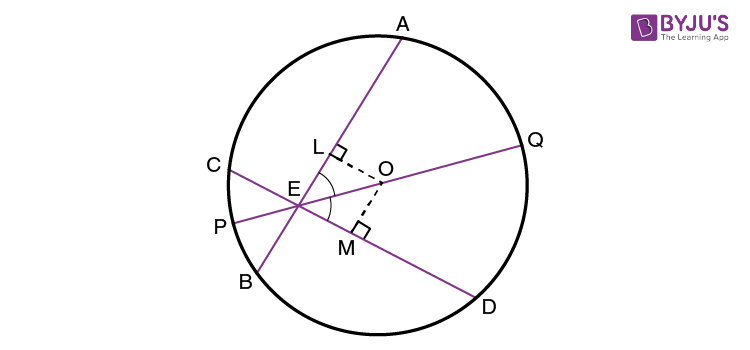
Given: AB and CD are the two chords of a circle with centre “O”. The intersection of these two chords is “E”. Now, PQ is the diameter of a circle, which passes through the point, such that  ∠AEQ = ∠DEQ. 

Now, we need to prove AB = CD. To prove this, draw the perpendiculars OL and OM on the chords AB and CD respectively.

By using the angle sum property of a triangle, we can write:

∠LOE = 180° – 90° – ∠LEO = 90° – ∠LEO

Therefore,

=90° – ∠AEQ = 90° – ∠DEQ

= 90° – ∠MEO = ∠MOE

From the triangles, OLE and OME,

∠LEO = ∠MEO

∠LOE = ∠MOE

EO = EO (Common)

Hence, ∆ OLE ≅ ∆ OME, Which means that OL = OM

Thus, the chord AB and CD are equal. 

Hence, proved.

Example 3: 

Two circles intersect at two points A and B, and AC and AD are the diameters of the circle. Show that the point B lies on the line segment DC.

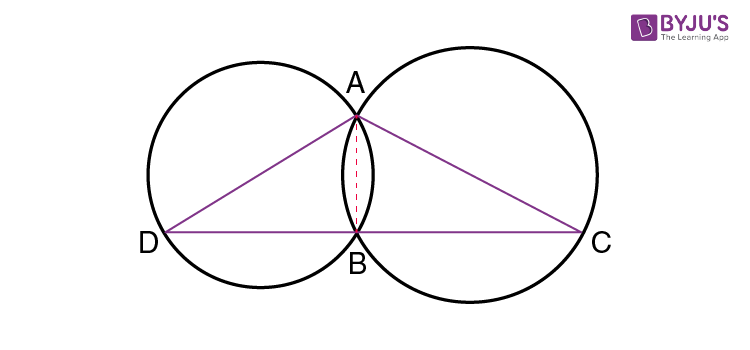
Solution:

From the given figure, join the points A and B.

Now, ∠ABD = 90° and ∠ABC = 90° (Angle in a semicircle)

Therefore, ∠ABD + ∠ABC = 90° + 90° = 180°

Now, DBC is a line. It means that point B lies in the line segment DC.

Hence, proved.

Practice Problems

1.  Prove that the segments of one chord are equal to corresponding segments of the other chord if two equal chords of a circle intersect within the circle.
2. ABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70°, ∠BAC is 30°, then determine ∠ BCD. Also, if AB = BC, find ∠ECD.
3. Show that a cyclic parallelogram is a rectangle. 

To learn all the class-wise topics, download BYJU’S – The Learning App and watch personalized videos to learn with ease.