Conjunction
Logical reasoning is an important skill used in all the fields such as science, engineering, and even in our daily life activities. It is also used in mathematical problem-solving strategies. One can quickly get the conclusion using the mathematical principles and the given facts. We know that there are different logical connections used in Maths to solve the problem. The commonly used logical connectives are:
- Negation
- Conjunction
- Disjunction
- Implication
- Equivalence
In this article, let us discuss in detail about one of the connectives called “Conjunction” with its definition, rules, truth table, and examples.
Conjunction Definition
When two statements are connected with an ‘AND’ gate, we can say that they have conjunction. For conjunctions, when both statements are true, then only the combined compound statement is true.
Suppose ‘parallelograms are rectangles’ and ‘circles are curves’ as our two statements. Let us combine them with ‘and’ to make the compound statement such as ‘parallelograms are rectangles and circles are curves’. This new compound statement is true only when the two statements we began with are true. If only one is false, and the other is true, the compound statement will be false.
For example, the same would be true if two statements were ‘Jessi likes cold coffee,’ and ‘Sony likes milkshake.’ If we combined them with ‘and’ to make ‘Jessi likes cold coffee and Sony likes milkshake,’ then the two statements must be true for the compound statement.
Conjunction in Maths
A conjunction is a statement formed by adding two statements with the connector AND. The symbol for conjunction is ‘∧’ which can be read as ‘and’. When two statements p and q are joined in a statement, the conjunction will be expressed symbolically as p ∧ q. If both the combining statements are true, then this statement will be true; otherwise, it is false.
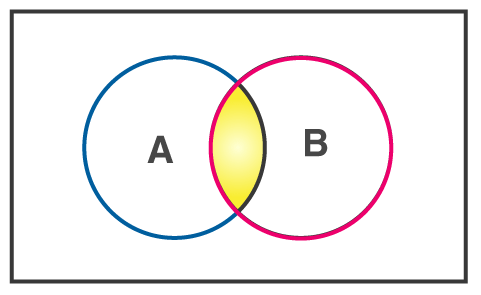
The below figure shows the conjunction of A and B:
Rules for a Conjunction
- The conjunction statement will only be true if both the combining statements are true otherwise, false.
- It is similar to an AND gate which is utilized under the topic Gate logic.
- Let p and q be the two statements. The compound statement p ∧ q is called the conjunction of p and q.
- The symbol “∧” that denotes the conjunction, it is read as “and” which is the logical connective.
Conjunction Truth Table
Let us make a truth table for P and Q, i.e. P ∧ Q.
| P | Q | P ∧ Q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
In this table, we can say that the conjunction is true only when both P and Q are true. If they are not, then the conjunction statement will be false.
Conjunction Examples
Example 1:
Let r: 5 be a rational number and s: 15 be a prime number. Is it a conjunction?
Solution:
Given that r: 5 is a rational number. This proposition is true.
s: 15 is a prime number. This proposition is false as 15 is a composite number.
Therefore, as per the truth table, r and s is a false statement.
So, r ∧ s = F
Example 2:
Let a: x be greater than 9 and b: x be a prime number. Is it a conjunction?
Solution:
Since x is a variable whose value we don’t know. Let us define a range for a and b.
To find the range let us take certain values for x;
When x= 6: a and b is false. Hence, a ∧ b is false.
When x= 3: a is false but b is true. But still, a ∧ b is false.
When x= 10: a is true but b is false. But still, a ∧ b is false.
When x= 11: a is true and b is true. Hence, a ∧ b is true.
Hence the conjunction a and b is only true when x is a prime number greater than 9.
To learn more Maths-related concepts, register with BYJU’S – The Learning App and subscribe to BYJU’S YouTube channel and learn in an engaging and fun way.