Construction of angles is one of the essential part of geometry. An angle is a shape formed by two rays (called arms of angle) that shares a common point (called vertex). We can use protractor to construct various types of angles. Also, there are methods by which we can construct some specific angles such as 60°, 30°, 120°, 90°, 45°, etc., without using protractor. Hence, these angles can be constructed using a compass and ruler.

Construction is an important concept where we learn to construct angles, lines and different shapes, in geometry. In this article, we will learn to construct the angles using protractor, compass, ruler and pencil.

Types of Angles for Construction

Before talking about construction of angles, let us quickly recall the different classifications of angles in Mathematics.

Depending on the inclination between the two arms, the six different types of angles are:

• Acute angle (less than 90 degrees)
• Obtuse angle (more than 90 degrees)
• Right angle (exactly 90 degrees)
• Straight angle (equal to 180 degrees)
• Reflex angle (more than 180 degrees)
• Full rotation (equal to 360 degrees)

Construction of Angles Using Protractor

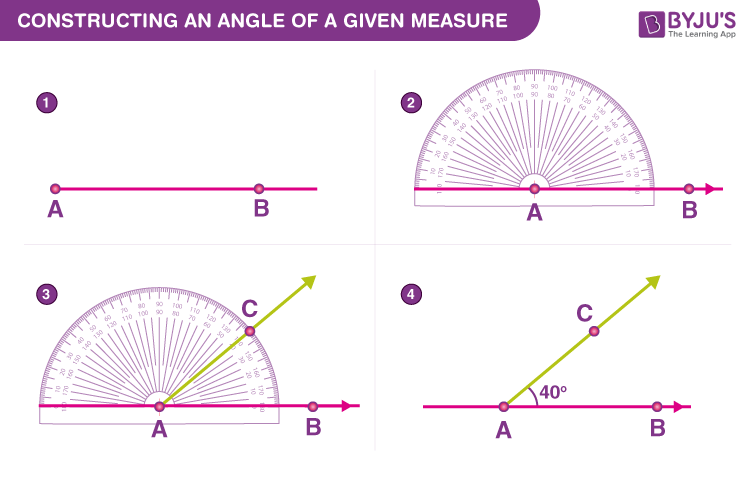
In our primary classes, we are taught to construct angles using protractors. It is easy to mark an angle of any measure using a protractor and construct it. We just need here a protractor, a ruler and a pencil. Let us see the steps of constructing angles using a protractor here.

• Step 1: Draw a line segment AB
• Step 2: Now place the center of the protractor on point A, such that the line segment AB is aligned with the line of the protractor
• Step 3: Starting from 0 (in the protractor) mark the point C in the paper as per the required angle.
• Step 4: Join points A and C. ∠BAC is the required angle

See the figure below to understand the steps.

Construction of Angles Using Compass and Ruler

Another method of constructing angles is by using a compass and a ruler. But we can use this method to construct some particular angles only such as 60°, 30°, 90°, 45°, etc. We can construct angles line 23°, 44°, 57°, etc., with accuracy using a compass and ruler. Let us construct few angles here using a compass.

Construction of angle 60 degrees (60°)

60 degrees is one of the most basic constructions, which facilitates constructing angles of several other measures. The steps are:

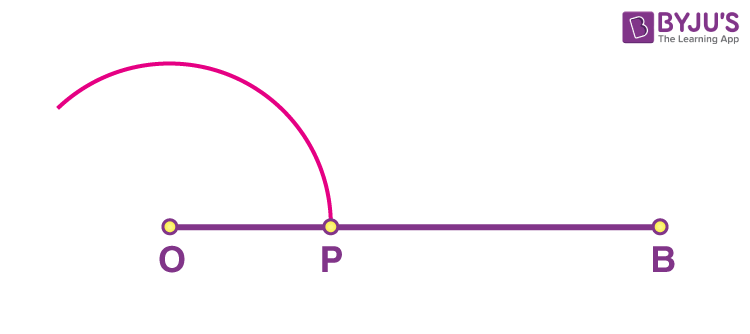
Step 1: Draw a line segment. Mark the left end as point O and the right end as point B.

Step 2: Take the compass and open it up to a convenient radius. Place its pointer at O and with the pencil-head make an arc which meets the line OB at say, P.

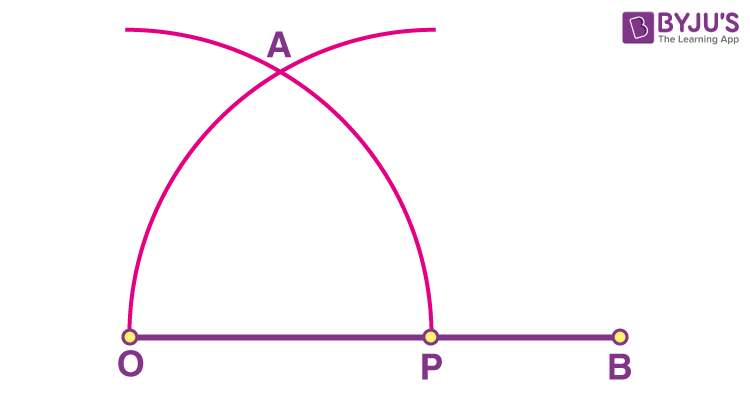
Step 3: Place the compass pointer at P and mark an arc that passes through O and intersects the previous arc at a point, say A.

Step 4: Draw a line from O through A.

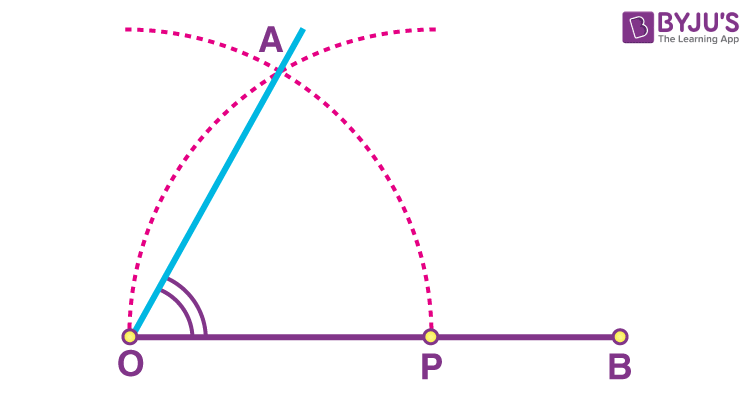
We get the required angle i.e. ∠AOB = 60-degree angle.

Construction of 30 degrees Angle (30°)

A 30-degree angle is half of the 60-degree angle.

• Follow the same steps as we have used for the construction of 60 degrees angles
• Bisect the angle into two equal parts
• Each part will be a 30-degree angle

Hence, a 30-degree angle is constructed.

Construction of angle 120 degrees (120°)

A 120-degree angle is twice the angle of 60-degree. The steps for construction of 120 degrees angle is given below:

Step 1: Draw a line segment. Mark the left end as point O and the right end as point B.

Step 2: Take the compass and open it up to a convenient radius. Place its pointer at O and with the pencil-head make an arc which meets the line OB at say, P.

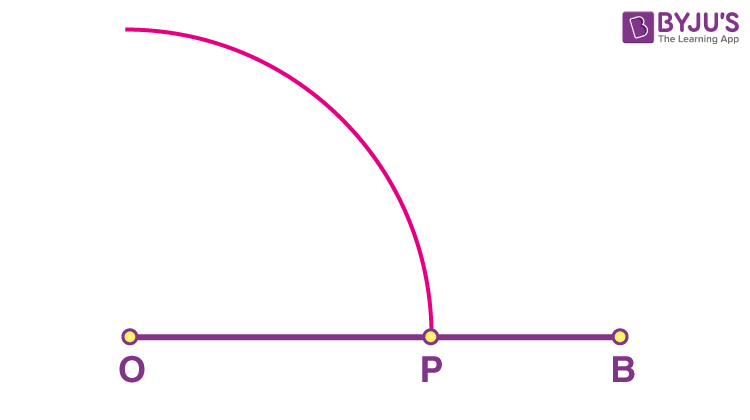
Step 3: Without disturbing the radius, place the pointer at P and make an arc that cuts the previous arc at a point, say Q.

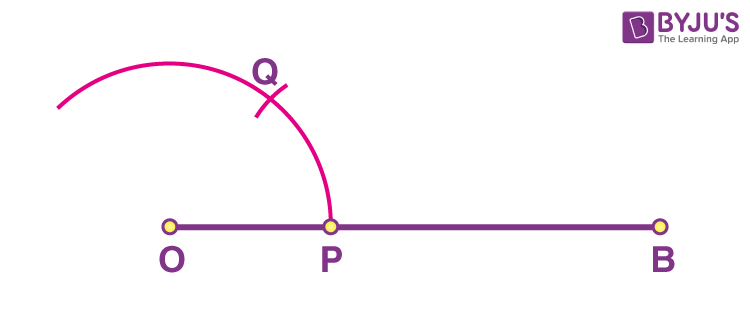
Step 4: Similarly, with the same radius on the compass, place the pointer at point Q. Mark another arc on the first arc. Mark the point where they intersect as A.

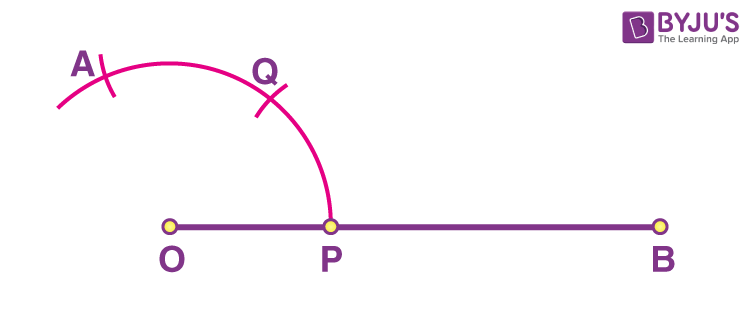
Step 5: Draw a line from O through A.

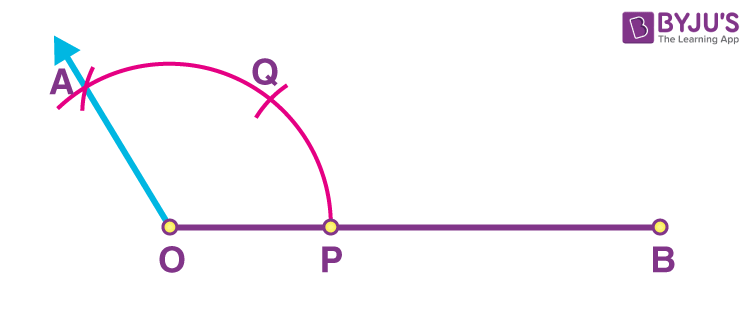
Hence,  ∠AOB is the required 120 degrees angle.

Construction of angle 90-degree (90°)

A 90-degree angle lies exactly between a 120-degree angle and a 60-degree angle. If we know the construction of 60 degrees and 120 degrees angles, then we can easily construct 90 degrees angle. Hence, follow the below steps:

• Draw a line segment OA
• Taking O as center and using a compass draw an arc of some radius, that cuts OA at B
• Taking B as center and with the same radius draw another arc, that cuts the first arc at C
• Taking C as center and with same radius draw an arc, that cuts the first arc at D
• Now taking C and D as centers and radius greater than the arc CD, draw two arcs, such that they intersect at E.
• Join OE such that ∠AOE is a 90-degree angle

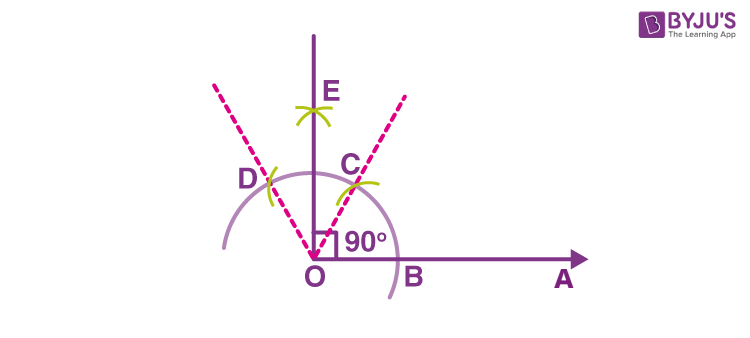
Hence, ∠AOE is the required 90-degree angle.

Solved Examples

Let us learn to construct more angles using a compass and a ruler.

Construction of angle 45-degree (45°)

A 45-degree angle is the half of 90° angle. Hence, follow the below steps to get the construct 45 degrees angle.

• Construct a 90-degree angle
• Construct an angle bisector that bisects the 90-degree angle into two equal parts.
• Each of the obtained angles is 45 degrees angle

Hence, a 45-degree angle is constructed

Construction of angle 75-degree (75°)

Angle 75 degrees can also be constructed using a compass and ruler.  Let us see the steps.

• Draw a line segment OA
• Taking O as center and using a compass draw an arc of some radius, that cuts OA at C
• Taking C as center and with the same radius draw another arc, that cuts the first arc at M
• Taking M as center and with same radius draw an arc, that cuts the first arc at L
• Now taking L and M as centers and radius greater than the arc LM, draw two arcs, such that they intersect at B.
• Join OB such that ∠AOB is a 90-degree angle
• Now taking N and M as centers, draw two arcs cutting at point P
• Join OP

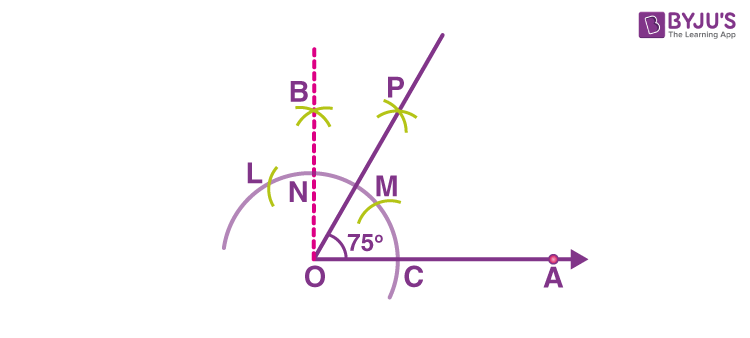
Hence, ∠AOP is the required 75 degrees angle.

Construction of angle 150 degrees

150 degrees is equal to the sum of angles 30 degrees and 120 degrees.

30° + 120°  = 150°

Thus, steps to construct the 150 degrees angle are:

• Construct angle ∠AOC = 120
• Extend AO to OB
• ∠BOC is equal to 60-degree angle (Since AOB = ∠AOC + ∠BOC = 180 degrees)
• Bisect the angle ∠BOC to form ∠COB = 30 

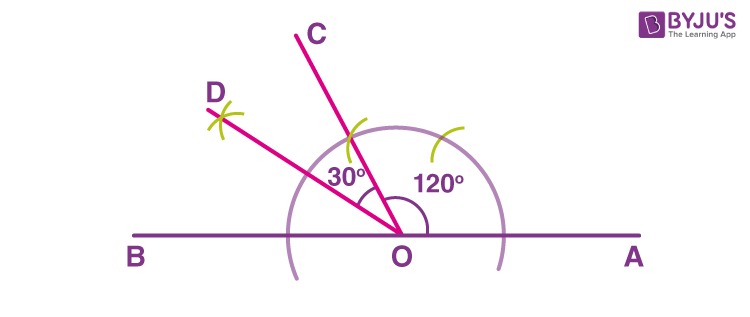
Hence, ∠AOD is the 150-degree angle. 

Video Lesson on Construction of Angles

Practice Question on Construction of Angles

1. Construct an angle of 135 degrees using a compass.
2. Construct a 105-degree angle using a compass.
3. Construct a 210-degree angle using a protractor.
4. Construct a 245-degree angle using a compass and a ruler

From the above discussion, one would be able to understand the importance of special angles in the field of geometry. To learn more about constructing angles of different measures, download BYJU’S- The Learning App.