In Geometry, a tangent is a line that touches the curve exactly at a point. The point is called the point of tangency. The tangent to a circle is defined as the perpendicular to the radius at the point of tangency. In this article, we are going to discuss what is tangent to a circle, how to construct a tangent to a circle, and also we will learn how to draw a tangent from the point outside of the circle with a step by step procedure.

What is Tangent to a Circle?

Tangent of a circle is a line which touches the circle exactly at one point. The point at which tangent touches the circle is known as ‘point of contact’. The radius of the circle and tangent are perpendicular to each other at the point of contact.

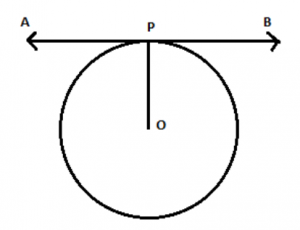
We know that, there cannot be any tangent drawn to the circle through a point inside the circle.

There can be only one tangent to a point on the circle.

Construction of Tangents to a Circle

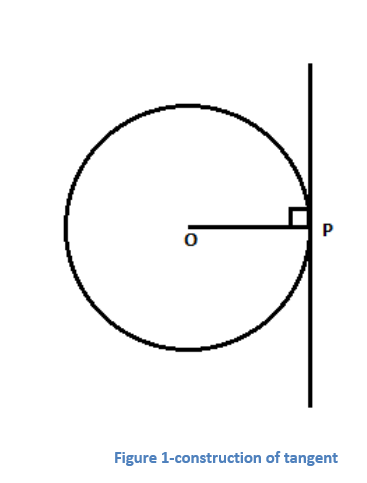
Let’s see how to draw a tangent to a circle at a point on the circle. (Refer fig.)

Step 1: Draw a circle with the required radius with centre O

Step 2: Join centre of the circle O and any point P on the circle. OP is the radius of the circle

Step 3: Draw a line perpendicular to radius OP through point P. This line will be a tangent to the circle at P

Two tangents can be drawn to a circle from a point outside of the circle. Lengths of the two tangents will be equal.

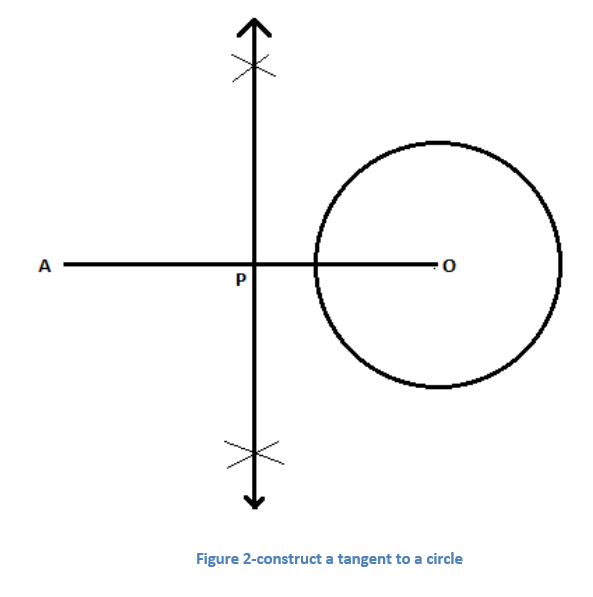
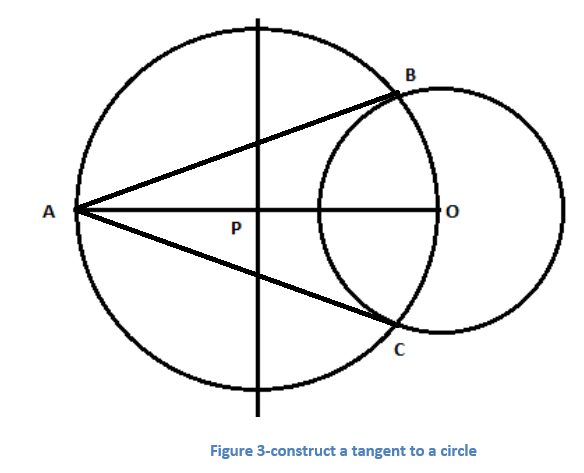
Construction of Two Tangents from a Point Outside of the Circle

Step 1:Consider a point A from the outside the circle with centre O.

Step 2: Join points A and O, bisect the line AO. Let P be the midpoint of AO.

Step 3: Draw a circle taking P as centre and PO as a radius. This circle will intersect at two points B and C on the circle with centre O.

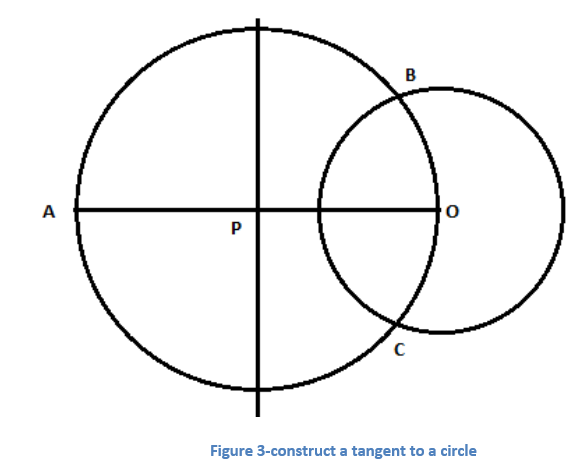Step 4: Join the point A with B and C. AB and AC are the required tangents through points B and C on the circle.

Why AB and AC are Tangents to the Circle with Centre O?

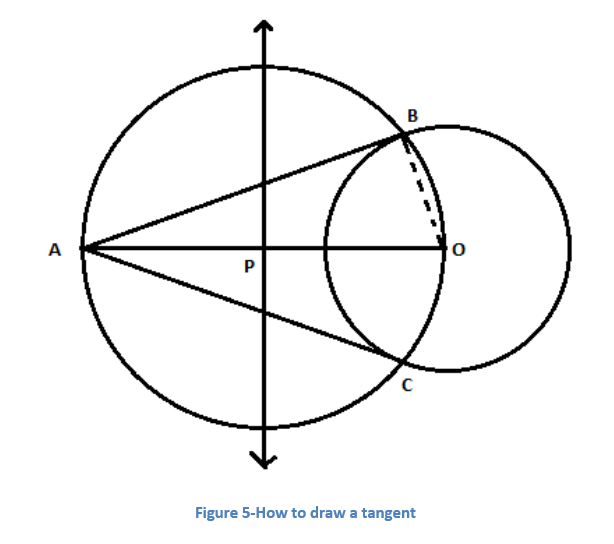
Join BO. It is observed that AO is a diameter of the circle with centre P. By construction, ∠ABO is an angle in a semi-circle.

Therefore,

∠ABO = 90°

Since OB is the radius of the circle with centre O, AB has to the tangent through the point B.

Similarly, AC is the tangent through the point C.

Note:

When the centre of the circle is not given to draw a tangent to the circle from a point outside the circle (Refer fig),

• Draw two non-parallel chords AB and CD.
• Draw perpendicular bisector for both AB and CD.
• The point O at which these bisectors intersect will be the centre of the circle because the radius is perpendicular bisector to chord.

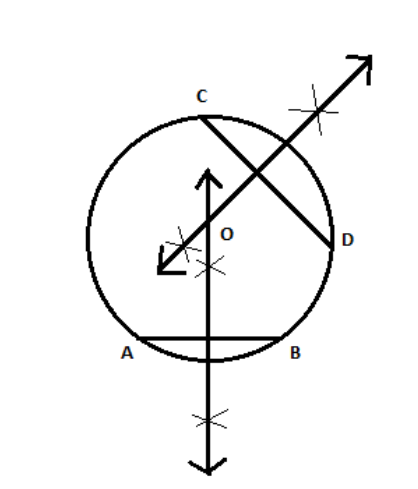
• Now, follow the steps to draw tangents when the centre is given.

To know more about constructions, log onto www.byjus.com and keep learning. To watch interesting videos on the topic, download BYJU’S – The Learning App from Google Play Store.