In trigonometry, the Cosine Rule says that the square of the length of any side of a given triangle is equal to the sum of the squares of the length of the other sides minus twice the product of the other two sides multiplied by the cosine of angle included between them. Cosine rule is also called law of cosines or Cosine Formula.

Suppose, a, b and c are lengths of the side of a triangle ABC, then;

where ∠x, ∠y and ∠z are the angles between the sides of the triangle. 

The cosine rule relates to the lengths of the sides of a triangle with any of its angles being a cosine angle. With the help of this rule, we can calculate the length of the side of a triangle or can find the measure of the angle between the sides.

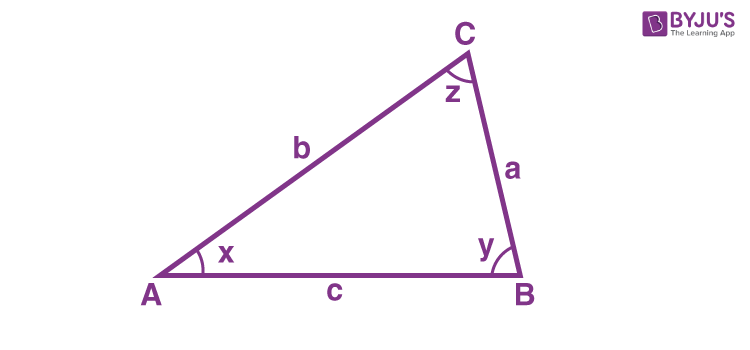
What are the Laws of Cosine?

As per the diagram, Cosine rules to find the length of the sides a, b & c of the triangle ABC is given by;

• a² = b² + c² – 2bc cos x
• b² = a² + c² – 2ac cos y
• c² = a² + b² – 2ab cos z

Similarly, to find the angles x, y and z, these formulae can be re-written as :

• cos x = (b² + c² -a²)/2bc
• cos y = (a² + c² -b²)/2ac
• cos z = (a² + b² – c²)/2ab

Also, read:

• Cosine Function
• Inverse Cosine

Proof

The law of cosine states that for any given triangle say ABC, with sides a, b and c, we have;

c² = a² + b² – 2ab cos C

Now let us prove this law.

Suppose a triangle ABC is given to us here. From the vertex of angle B, we draw a perpendicular touching the side AC at point D. This is the height of the triangle denoted by h.

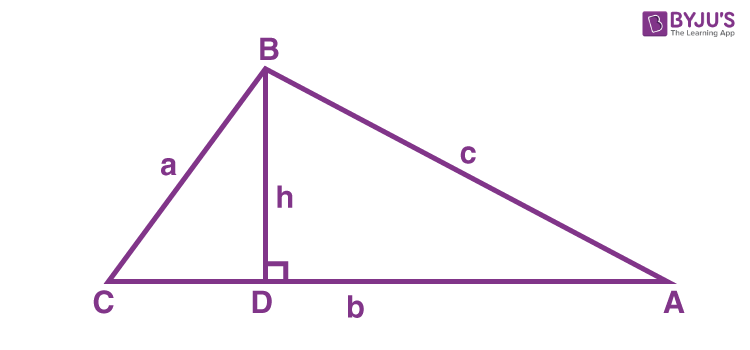
Now in triangle BCD, as per the trigonometry ratio, we know;

cos C = CD/a       [cos θ = Base/Hypotenuse]

or we can write;

CD = a cos C ………… (1)

Subtracting equation 1 from side b on both the sides, we get;

b – CD = b – a cos C

or

DA = b – a cos C

Again, in triangle BCD, as per the trigonometry ratio, we know;

sin C = BD/a      [sin θ = Perpendicular/Hypotenuse]

or we can write;

BD = a sin C ……….(2)

Now using Pythagoras theorem in triangle ADB, we get;

c² = BD² + DA²        [Hypotenuse² = Perpendicular² + Base² ]

Substituting the value of DA and BD from equation 1 and 2, we get;

c² = (a sin C)² + (b – a cos C)²

c² = a² sin²C + b² – 2ab cos C + a² cos² C

c² = a² (sin²C + cos² C)  + b² – 2ab cos C

By trigonometric identities, we know;

sin²θ+ cos²θ = 1

Therefore,

c² = a²  + b² – 2ab cos C

Hence, proved.

Cosine Formula

The formula to find the sides of the triangle using cosine rule is given below:

• \(a = \sqrt{b^2 + c^2 – 2~b~c~ cos x}\)
• \(b = \sqrt{a^2 + c^2 – 2~a~c~ cos y}\)
• \(c = \sqrt{a^2 + b^2 – 2~a~b~cos z}\)

Sine Formula

As per sine law, 

a / Sin A= b/ Sin B= c / Sin C

Where a,b and c are the sides of a triangle and A, B and C are the respective angles. 

Also, we can write:

a: b: c = Sin A: Sin B: Sin C

Solved Example

Find the length of x in the following figure.

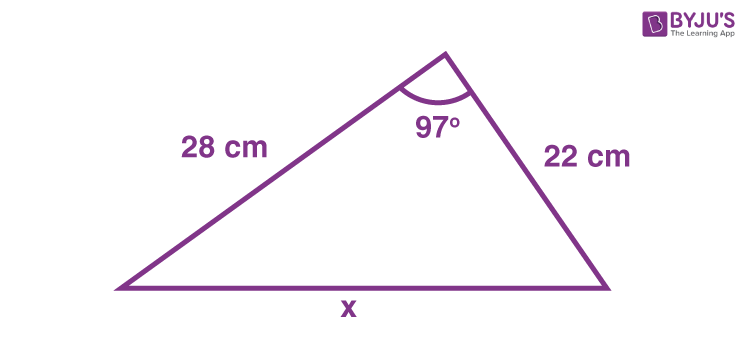
Solution: By applying the Cosine rule, we get:

x² = 22² +28² – 2 x 22 x 28 cos 97

x² = 1418.143

x = √ 1418.143

Learn more about different Math topics with BYJU’S – The Learning App