Derivatives are defined as the varying rate of change of a function with respect to an independent variable. The derivative is primarily used when there is some varying quantity, and the rate of change is not constant. The derivative is used to measure the sensitivity of one variable (dependent variable) with respect to another variable (independent variable). In this article, we are going to discuss what are derivatives, the definition of derivatives Math, limits and derivatives in detail.

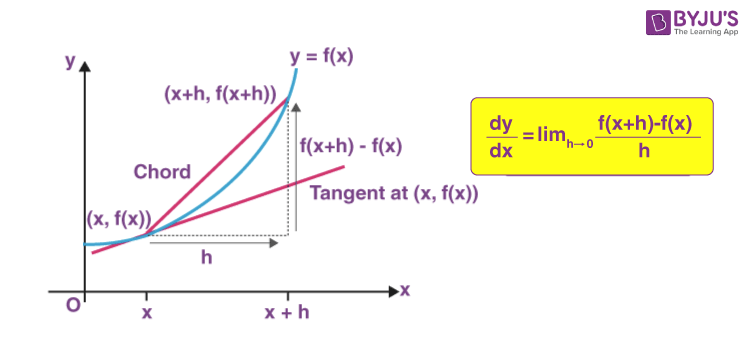
Table of Contents:

• Meaning
• Derivatives in Maths
• Formulas
• Types
• Derivatives of Trigonometric Functions
• Derivative of tanx
• Derivative of 1 x
• Properties
• Examples
• FAQs

Derivatives Meaning

Derivatives in Maths refers to the instantaneous rate of change of a quantity with respect to the other. It helps to investigate the moment by moment nature of an amount.

Derivative Example:

Let a car takes ‘t’  seconds to move from a point ‘a’ to ’b’.

But how long will it take to move from point ‘a’ to ‘c’?

Or

How much distance will it cover in ‘t-1’ seconds?

This can be known from the velocity that is as follows:

Velocity (v) = d(x)/d(t)

Where ‘x’ is the distance travelled and ‘t’ is the time taken to cover that distance.

This will give you the distance covered per unit time so that we can analyze any distance covered in any interval of time.

Derivatives in Math – Calculus

The process of finding the derivative is called differentiation. The inverse process is called anti-differentiation. Let’s find the derivative of a function y = f(x).  It is the measure of the rate at which the value of y changes with respect to the change of the variable x. It is known as the derivative of the function “f”, with respect to the variable x.

If an infinitesimal change in x is denoted as dx, then the derivative of y with respect to x is written as dy/dx.

Here the derivative of y with respect to x is read as “dy by dx” or “dy over dx”

Example:

Let ‘y’ be a dependent variable and ‘x’ be an independent variable.

Consider a change in the value of x, that is dx.

This change in x will bring a change in y, let that be dy.

Now to find out the change in y with a unit change in x as follows:

Let f(x) be a function whose value varies as the value of x varies

Steps to find the Derivative:

1. Change x by the smallest possible value and let that be ‘h’ and so the function becomes f(x+h).
2. Get the change in value of function that is : f(x + h) – f(x)
3. The rate of change in function f(x) on changing from ‘x’ to ‘x+h’ will be

           \(\frac{dy}{dx} = lim_{h\rightarrow 0}\frac{f(x+h) – f(x)}{h}\)

Now d(x) is ignorable because it is considered to be too small.

Derivatives Formulas

The formulas of derivatives for some of the functions such as linear, exponential and logarithmic functions are listed below:

• d/dx (k) = 0, where k is any constant
• d/dx(x) = 1
• d/dx(xⁿ) = nx^n-1
• d/dx (kx) = k, where k is any constant
• d/dx (√x) = 1/2√x
• d/dx (1/x) = -1/x²
• d/dx (log x) = 1/x, x > 0
• d/dx (e^x) = e^x
• d/dx (a^x) = a^x log a

Derivatives Types

Derivatives can be classified into different types based on their order such as first and second order derivatives. These can be defined as given below.

First-Order Derivative

The first order derivatives tell about the direction of the function whether the function is increasing or decreasing. The first derivative math or first-order derivative can be interpreted as an instantaneous rate of change. It can also be predicted from the slope of the tangent line.

Second-Order Derivative

The second-order derivatives are used to get an idea of the shape of the graph for the given function. The functions can be classified in terms of concavity. The concavity of the given graph function is classified into two types namely:

• Concave Up
• Concave Down

Calculus-Derivative Example

Let f(x) be a function where f(x) = x²

The derivative of x² is 2x, that means with every unit change in x, the value of the function becomes twice (2x).

Limits and Derivatives

When dx is made so small that is becoming almost nothing. With Limits, we mean to say that x approaches zero but does not become zero.

Mathematically: for all real ε > 0 there exists a real  δ > 0 such that for all x with 0 < |x − c| < δ, (here c ∈ R) we have |f(x) − L| < ε

Key Concepts

• To differentiate a power of x that is in the denominator, first express it as a power with a negative exponent. Eg. \(\frac{1}{x^{2}}= x^{-2}\)
• Derivative rules simplify the process of differentiating polynomial functions.
• To differentiate a radical, first, express it as a power with a rational exponent

Apply Derivative Rules to Solve an Instantaneous Rate of Change Problem

A skydiver jumps out of a plane from a height of 2200 m. The skydiver’s height above the ground, in meters, after t seconds is represented by the function h(t) = 2200 – 4.9t² (assuming air resistance is not a factor). How fast is the skydiver falling after 4 s?

Solution

The instantaneous rate of change of the height of the skydiver at any point in time is represented by the derivative of the height function.

h(t) = 2200 – 4.9t²

h'(t) = 0 – 4.9 (2t) = -9.8 t

Substitute t = 4 into the derivative function to find the instantaneous rate of change at 4 s.

h'(t) = – 9.8 (4) = -39.2

After 4 s, the skydiver is falling at a rate of 39.2 m/s.

Derivatives of Trigonometric Functions

We can also find the derivative of trigonometric functions that means for sin, cos, tan and so on. The formulas are given below:

• d/dx (sin x) = cos x
• d/dx (cos x) = -sin x
• d/dx (tan x) = sec²x
• d/dx (cosec x) = -cosec x cot x
• d/dx (sec x) = sec x tan x
• d/dx (cot x) = -cosec²x

Derivative of tan x

The derivative of tan x can be derived using the quotient rule as shown below:

Let f(x) = tan x 

We know that tan x = sin x/ cos x

Let us take u = sin x and v = cos x

As we know,

d/dx (u/v) = [v(du/dx) – u(dv/dx)]/ v²

d/dx (sin x/cos x) = [cos x(d/dx)sin x – sin x(d/dx)cos x]/ cos²x

= [cos x . cos x – sin x . (-sin x)]/cos²x

= (cos²x + sin²x)/cos²x

Using the identity sin²A + cos²A = 1,

= 1/cos²x

= sec²x [since 1/cos x = sec x]

d/dx (tan x) = sec²x

Therefore, the derivative of tan x is sec²x.

Derivative of 1/x

The derivative of 1/x can be derived as given below:

d/dx (1/x) = d/dx (x^-1)

We know that d/dx (xⁿ) = nx^{n – 1}

Here, n = -1

d/dx(1/x) = d/dx (x^-1) = (-1)x^{(-1 – 1)}

= -x^-2

= -1/x²

Hence, the derivative of 1/x is -1/x².

Properties of Derivatives

Derivatives can be divided into smaller parts so that the given expressions can be easily evaluated. In the process of splitting the expressions or functions, the terms are separated based on the operator such as plus (+), minus (-) or division (/). This can be better understood using the examples given below.

Derivatives Examples

Example 1: Find the derivative of the function f(x) = 5x² – 2x + 6.

Solution:

Given,

f(x) = 5x² – 2x + 6

Now taking the derivative of f(x),

d/dx f(x) = d/dx (5x² – 2x + 6)

Let us split the terms of the function as:

d/dx f(x) = d/dx (5x²) – d/dx (2x) + d/dx (6)

Using the formulas:

d/dx (kx) = k and d/dx (xⁿ) = nx^{n – 1}

⇒ d/dx f(x) = 5(2x) – 2(1) + 0 = 10x – 2

Example 2: Find the derivative of 2 tan x + 1

Solution:

Let the given function be f(x) = 2 tan x + 1

Now, taking the derivative,

d/dx f(x) = d/dx (2 tan x + 1)

= d/dx (2 tan x) + d/dx (1)

= 2 (sec²x) + 0

= 2 sec²x

For more Maths-related concepts, download  BYJU’S – The Learning App and also watch interactive videos to learn with ease.