A direct and inverse proportion are used to show how the quantities and amount are related to each other. They are also mentioned as directly proportional or inversely proportional. The symbol used to denote the proportionality is ‘∝‘.  For example, if we say, a is proportional to b, then it is represented as “a ∝ b” and if we say, a is inversely proportional to b, then it is denoted as ‘a∝1/b’. These relations are governed by some proportionality rules. Now in both cases, the value of ‘a’ changes in terms of ‘b’ or when the value of ‘b’ changes, the value of ‘a’ also get changed. The change in both values is equated with a constant of proportionality. Basically, a proportion states that two ratios like a/b and c/d are equal to each other, in such a way, a/b = c/d. In this article, we will learn the definition, examples and also will solve some questions based on the concept.

Direct and Inverse Proportion Definitions

The proportion is said to be a direct proportion between two values when one is a multiple of the other.

For example, 1 cm is equal to 10 mm.

Here, in order to convert cm to mm, the multiplier should be 10.

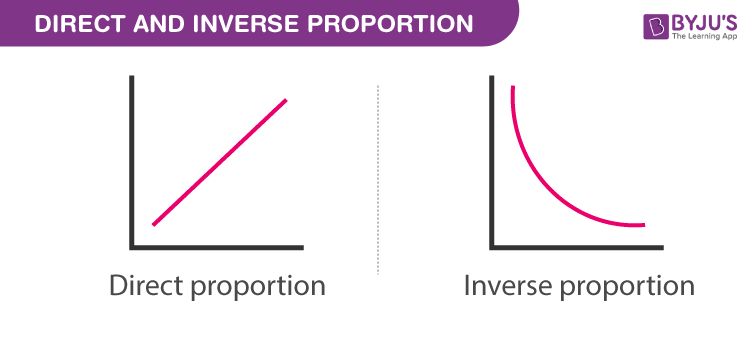
Direct Proportion

Two quantities a and b are said to be in direct proportion if they increase or decrease together. In other words, the ratio of their corresponding values remains constant. This means that,

a/ b = k

where k is a positive number, then the quantities a and b are said to vary directly.

In such a case if the values b₁, b₂ of b corresponding to the values a₁, a₂ of a, respectively then it becomes;

a_1//b₁ = a₂ /b₂

The direct proportion is also known as direct variation.

Directly Proportion Symbol

The symbol used to represent the direct proportion is “∝”.

Consider the statement,

a is directly proportional to b

This can be written using the symbol as:

a ∝ b

Consider the other statement, a = 2b

In this case, it shows that a is proportional to b, and the value of one variable can be found if the value of other variable is given.

For example: 

Let b=7

Therefore, a = 2 x 7 = 14

Similarly, if you take the value of “a” as 14, you will find the value of b

Such that

14 = 2 x b

14/ 2 = b

Therefore, b=7

Inverse Proportion

The value is said to inversely proportional when one value increases, and the other decreases. The proportionality symbol is used in a different way. Consider an example; we know that the more workers on a job would reduce the time to complete the task. It is represented as:

Number of workers ∝ (1/ Time taken to complete the job)

Inverse Proportion Definition

Two quantities a and b are said to be in inverse proportion if an increase in quantity a, there will be a decrease in quantity b, and vice-versa. In other words, the product of their corresponding values should remain constant.  Sometimes, it is also known as inverse variation

That is, if ab = k, then a and b are said to vary inversely. In this case, if b₁, b₂ are the values of b corresponding to the values a₁, a₂ of a, respectively then a₁ b₁ = a₂ b₂ or a₁/a₂ = b₂ /b₁

The statement ‘a is inversely proportional to b is written as

a ∝ 1/b

Here, an equation is given that involves the inverse proportions that can be used to calculate the other values.

Let,

a = 25/b

Here a is inversely proportional to b

If one value is given, the other value can be easily found.

Say b=10

a= 25/10 = 2.5

Similarly, if a = 2.5, the value of b can be obtained.

2.5 = 25/b

b= 25/2.5 = 10

How to Write Direct and Indirect Proportion Equation?

If we have to write a proportionality whether it is direct or indirect in an equation, follow the below steps:

• Step 1: First, write down the proportional symbol
• Step 2: Convert it as an equation using the constant of proportionality
• Step 3: Find the constant of proportionality from the given information
• Step 4: After finding the constant of proportionality, substitute in an equation

Direct and Inverse Proportion Solved Examples

Below are examples to understand the concept of direct and inverse proportion in a better way.

Example 1:

A train is moving at a uniform speed of 75 kilometres/hour.

(i)How many kilometres are covered by train in 20 minutes?

(ii) Find the time required to cover a distance of 250 kilometres.

Solution:

Let the distance travelled (in km) in 20 minutes be a and time taken (in minutes) to cover 250 km be b.

We know that 1 hour = 60 minutes

Since the speed of the train is uniform, therefore, the distance covered would be directly proportional to time.

(i) We have 75 /60 = a /20

or (75 /60) 20 = a

or a = 25

So, the train will cover a distance of 25 kilometres in 20 minutes.

(ii) Also, 75/60=250/ b or

b=(250 x 60)/ 75

b = 200 minutes or 3 hours 20 minutes.

Therefore, 3 hours 20 minutes is required to cover a distance of 250 kilometres.

Alternatively, when a is known, then one can determine b, using the relation

a/20 =250/ b

Example 2:

The value f is directly proportional to g. When f = 20, g = 10. Find an equation relating f and g.

Solution:

Given, f ∝ g

or we can write,

f = kg, where k is the constant proportionality.

20 = k x 10

k = 2

Therefore, the required equation is;

f = 2g

Practice Questions

1. A car is moving at a speed of 60 Km/hr. How far will it travel in 30 minutes?
2. If the cost of 10 pens is Rs.120, how much will it cost for 15 pens?
3. If 15 workers can do work in 12 days, then how many workers will complete the same work in 6 days?

For more information and topic-related questions, register with BYJU’S – The Learning App and watch interactive videos to learn with ease.