The distance between two lines means that the parallel lines can be determined from one point to another on the opposite line. It is often referred to as the shortest distance between two parallel lines or the perpendicular distance between two lines. In coordinate geometry, we have several formulas, out of which distance formula is one of the most commonly used formulas. In this article, you will learn how to derive the formula for distance between two lines and the distance of a point from a line along with examples.

Distance Between Two Lines in Coordinate geometry

The distance between any two parallel lines can be determined by the distance of a point from a line, and it is equivalent to the length of the vertical distance from any point on one of the lines to another line. So let’s understand how to derive the formula for the distance of a line from a point.

Distance Between Point and Line Derivation

The general equation of a line is given by Ax + By + C = 0. 

 Consider a line L : Ax + By + C = 0 whose distance from the point P (x₁, y₁) is d.

Draw a perpendicular PM from the point P to the line L, as shown in the figure below.

Let Q and R be the points where the line meets the x-and y-axes, respectively.

Coordinates of the points can be written as Q(-C/A, 0) and R(0, -C/B).

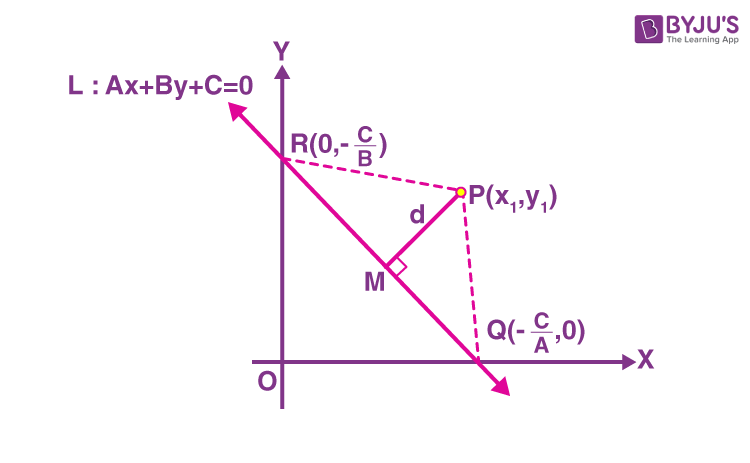
Let’s derive the formula using the formulas of the area of the triangle in different aspects.

In triangle PQR,

ar(ΔPQR) = (1/2) × Base × Height = (1/2) × PM × QR

⇒ PM = [2 ar(ΔPQR)]/2….(i)

In coordinate geometry, the area of triangle with vertices (x₁, y₁), (x₂, y₂) and (x₃, y₃) is

Δ = (1/2) |x₁(y₂ – y₃) + x₂(y₃ – y₁) + x₃(y₁ – y₂)|

Here,

(x₁, y₁) = P(x₁, y₁)

(x₂, y₂) = Q(-C/A, 0)

(x₃, y₃) = R(0, -C/B)

Now, by substituting these values in area formula, we get;

ar(ΔPQR) = (1/2) |x₁(0 + C/B) + (-C/A)(-C/B – y₁) + 0(y₁ – 0)|

ar(ΔPQR) = (1/2) |x₁(C/B) + (C²/AB) + y₁(C/A)|

⇒ 2 ar(ΔPQR) = |C/AB| . |Ax₁ + By₁ + C|….(ii)

Distance QR = √[(0 + C/A)² + (C/B – 0)²]

= √[(C²/A²) + (C²/B²)]

Let’s find QR using the distance formula.

QR = |C/AB| √(A² + B²)….(iii)

Substituting (ii) and (iii) in (i),

PM = [|C/AB| . |Ax₁ + By₁ + C|] / [|C/AB| √(A² + B²)]

d = |Ax₁ + By₁ + C|]/ √(A² + B²)

Therefore, the perpendicular distance (d) of a line Ax + By+ C = 0 from a point (x₁, y₁) is given by

d = |Ax₁ + By₁ + C|]/ √(A² + B²)

Based on this formula, we can derive the formula for the distance between two parallel lines.

Distance Between Two Parallel Lines

The distance between two parallel lines is equal to the perpendicular distance between the two lines. We know that the slopes of two parallel lines are the same; therefore, the equation of two parallel lines can be given as:

yy = mx + c₁….(1)

and yy = mx + c₂….(2)

The point AA is the intersection point of the second line on the x-axis.

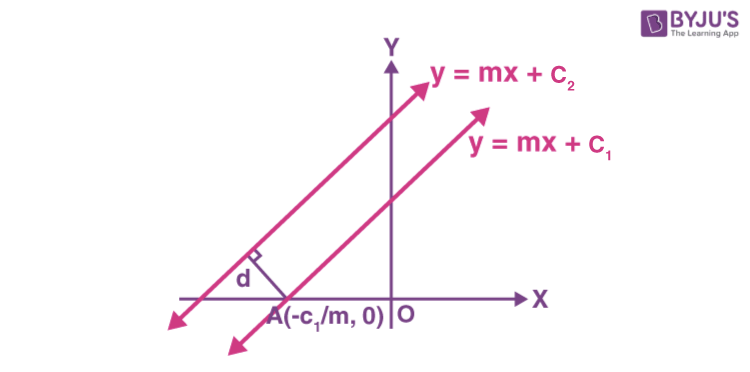
The perpendicular distance would be the required distance between two lines

The distance between the point \(A\) and the line \(y\) = \(mx ~+ ~c_2\) can be given by using the formula:

\(d\) = \(\frac{\left | Ax_{1} + By_{1} + C \right |}{\sqrt{A^{2} + B^{2}}}\)

\(\Rightarrow d \) \(= \frac{\left | (-m)(\frac{-c_{1}}{m}) –  c_{2} \right |}{\sqrt{1 + m^{2}}}\)

\(\Rightarrow d \) \(= \frac{\left | c_{1} – c_{2} \right |}{\sqrt{1 + m^{2}}}\)

Thus, we can conclude that the distance between two parallel lines is given by:

\(d\) = \(\frac{|c_1 ~- ~c_2|}{√1 + m^2}\)

If we consider the general form of the equation of straight line, and the lines are given by:

\( L_1 ~: ~Ax~ + ~By ~+ ~C_1\) = \(0\)

\( L_2 ~: ~Ax ~+ ~By ~+ ~C_2\) = \(0 \)

Then, the distance between them is given by:

\(d\) = \(\frac{|C_1 ~- ~C_2|}{√A^2~ +~ B^2}\)

Shortest Distance Between Two parallel Lines

The shortest distance between the two parallel lines can be determined using the length of the perpendicular segment between the lines. It does not matter which perpendicular line you are choosing, as long as two points are on the line.

Thus, we can now easily calculate the distance between two parallel lines and the distance between a point and a line.

Solved Examples

Example 1:

Find the distance between two lines 3x + 4y = 9 and 6x + 8y = 15.

Solution:

Given equations of lines are:

3x + 4y = 9….(i)

6x + 8y = 15 Or 3x + 4y = 15/2 ….(ii)

Let us check whether the given lines are parallel or not.

From (i),

4y  = -3x + 9

y = (-¾)x + (9/4)

Here, slope = m₁ = -¾

From (ii),

8y = -6x + 15

y = (-6/8)x + (15/8)

y = (-¾)x + (15/8)

Here, slope = m₂ = -¾

Thus, the slope of the given lines is equal so they are parallel to each other.

Now, by comparing with the standard form of parallel lines equations, we get:

A = 3, B = 4, C₁ = -9, C₂ = -15/2

d = |C₁ – C₂|/√(A² + B²)

= |-9 + (15/2)|/√(9 + 16)

= |-18 + 15|/2√25

= |-3|/(2 × 5)

= 3/10

Therefore, the distance between the given lines is 3/10 units.

Example 2: 

The distance between two parallel lines 5x – 12y + 2 = 0 and 5x – 12y + k = 0 is given by 5/13 units. Find the value of k.

Solution:

Given equations of lines are:

5x – 12y + 2 = 0….(i)

5x – 12y + k = 0 ….(ii)

Let us check whether the given lines are parallel or not.

From (i),

12y = 5x + 2

y = (5/12)x + (2/12)

Here, slope = m₁ = 5/12

From (ii),

From (i),

12y = 5x + k

y = (5/12)x + (k/12)

Here, slope = m₂ = 5/12

Thus, the slope of the given lines is equal so they are parallel to each other.

Now, by comparing with the standard form of parallel lines equations, we get:

A = 5, B = -12, C₁ = 2, C₂ = k

d = |C₁ – C₂|/√(A² + B²)

5/13 = |2 – k|/√(25 + 144)

5/13 = |2-k|/√169

5/13 = |2 – k|/13

5 = 2 – k

k = 2 – 5 = -3