The Dot Product of Vectors can be defined in two ways:

• Geometrically
• Algebraically

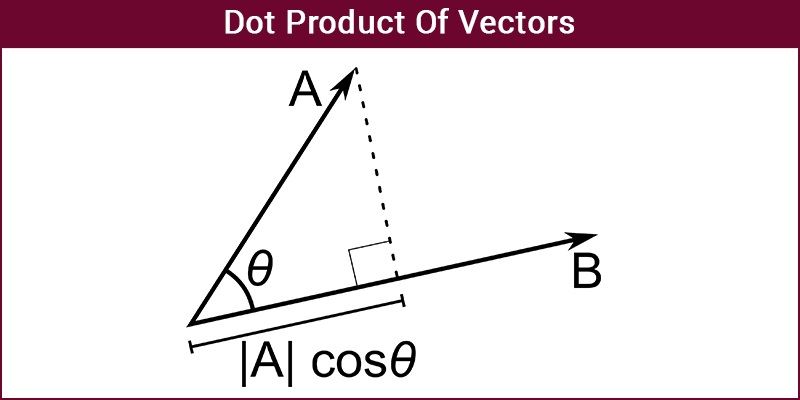
Dot Product – Geometrical Definition

The Dot Product of Vectors is written as a.b=|a||b|cosϴ

Where |a| and |b| are the magnitudes of vector a and b and ϴ is the angle between vector a and b.

If the two vectors are Orthogonal, i.e., the angle between them is 90 then a.b=0 as cos 90 is 0.

If the two vectors are parallel to each other the a.b=|a||b| as cos 0 is 1.

Dot Product – Algebraic Definition

The Dot Product of Vectors is written as

Dot product of vector – An example

Let there be two vectors [6,2,-1] and [5,-8,2]

a.b=(6)(5)+(2)(-8)+(-1)(2)

a.b=30-16-2

a.b=12

Let there be two vectors |a|=4 and |b|=2 and ϴ=60

a.b=|a||b|cos 60

a.b=4.2cos60

a.b=4

Dot Product of Vector – Properties

The following are the Vector properties:

Commutative property

a.b=b.a

a.b=|a||b|cosϴ

a.b=|b||a|cosϴ

Distributive property

a.(b+c)=a.b+a.c

Bilinear property

a.(rb+c)=r.(a.b)+(a.c)

Scalar Multiplication property

(xa).(yb)=xy(a.b)

Non-Associative property

Because a dot product between a scalar and a vector is not allowed

Orthogonal property

Two vectors are orthogonal only if a.b=0

Dot Product of Vector – Valued Functions

The dot product of vector-valued functions, r(t) and u(t) each gives you a vector at each particular “time” t, and so the function r(t)⋅u(t) is a scalar function.

Inferring, the dot product at each given t; this product precisely measures the relationship between r(t) and u(t).